359886
If \(W_{1}, W_{2}\) and \(W_{3}\) represent the work done in moving a particle from \(A\) and \(B\) along three different paths 1, 2 and 3, respectively (As shown in the figure) in the gravitational field of a point mass \(m\), find the correct relation
between \(W_{1}, W_{2}\) and \(W_{3}\).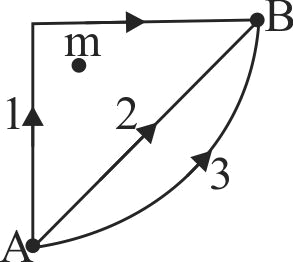
359887 If the gravitational field in the space is given as \(\left(-\dfrac{K}{r^{2}}\right)\). Taking the reference point to be at \(r = 2\;cm\) with gravitational potential \(V = 10\;J{\rm{/}}kg\). Find the gravitational potential at \(r = 3\;cm\) in SI unit (Given, that \(K = 6\,J\;cm/kg\))
359886
If \(W_{1}, W_{2}\) and \(W_{3}\) represent the work done in moving a particle from \(A\) and \(B\) along three different paths 1, 2 and 3, respectively (As shown in the figure) in the gravitational field of a point mass \(m\), find the correct relation
between \(W_{1}, W_{2}\) and \(W_{3}\).
359887 If the gravitational field in the space is given as \(\left(-\dfrac{K}{r^{2}}\right)\). Taking the reference point to be at \(r = 2\;cm\) with gravitational potential \(V = 10\;J{\rm{/}}kg\). Find the gravitational potential at \(r = 3\;cm\) in SI unit (Given, that \(K = 6\,J\;cm/kg\))
359886
If \(W_{1}, W_{2}\) and \(W_{3}\) represent the work done in moving a particle from \(A\) and \(B\) along three different paths 1, 2 and 3, respectively (As shown in the figure) in the gravitational field of a point mass \(m\), find the correct relation
between \(W_{1}, W_{2}\) and \(W_{3}\).
359887 If the gravitational field in the space is given as \(\left(-\dfrac{K}{r^{2}}\right)\). Taking the reference point to be at \(r = 2\;cm\) with gravitational potential \(V = 10\;J{\rm{/}}kg\). Find the gravitational potential at \(r = 3\;cm\) in SI unit (Given, that \(K = 6\,J\;cm/kg\))
359886
If \(W_{1}, W_{2}\) and \(W_{3}\) represent the work done in moving a particle from \(A\) and \(B\) along three different paths 1, 2 and 3, respectively (As shown in the figure) in the gravitational field of a point mass \(m\), find the correct relation
between \(W_{1}, W_{2}\) and \(W_{3}\).
359887 If the gravitational field in the space is given as \(\left(-\dfrac{K}{r^{2}}\right)\). Taking the reference point to be at \(r = 2\;cm\) with gravitational potential \(V = 10\;J{\rm{/}}kg\). Find the gravitational potential at \(r = 3\;cm\) in SI unit (Given, that \(K = 6\,J\;cm/kg\))
