359854 The following figure shows two shells of masses \(m_{1}\) and \(m_{2}\). The shells are concentric. At which point, a particle of mass \(m\) shall experience zero force?

359855 Intensity of gravitational field inside the hollow spherical shell is

359856 Assertion :
If earth were a hollow sphere, gravitational field intensity at any point inside the earth would be zero.
Reason :
Net force on a body inside the sphere is zero.

359857 A solid sphere of mass \(M\) and radius \(R\) has a spherical cavity of radius \(R / 2\) such that the centre of cavity is at a distance \(R / 2\) from the centre of the sphere. A point mass \(m\) is placed inside the cavity at a distance \(R / 4\) from the centre of sphere. The gravitational pull between the sphere and the point mass \(m\) is

359858 A very long (length \(L\)) cylindrical galaxy is made of uniformly distributed mass and has radius \(R(R < < L)\). A star outside the galaxy is orbiting the galaxy in a plane perpendicular to the galaxy and passing through centre if the time period of star is \(T\) and its distance from the galaxy's axis is \(r\), then :

359854 The following figure shows two shells of masses \(m_{1}\) and \(m_{2}\). The shells are concentric. At which point, a particle of mass \(m\) shall experience zero force?

359855 Intensity of gravitational field inside the hollow spherical shell is

359856 Assertion :
If earth were a hollow sphere, gravitational field intensity at any point inside the earth would be zero.
Reason :
Net force on a body inside the sphere is zero.

359857 A solid sphere of mass \(M\) and radius \(R\) has a spherical cavity of radius \(R / 2\) such that the centre of cavity is at a distance \(R / 2\) from the centre of the sphere. A point mass \(m\) is placed inside the cavity at a distance \(R / 4\) from the centre of sphere. The gravitational pull between the sphere and the point mass \(m\) is

359858 A very long (length \(L\)) cylindrical galaxy is made of uniformly distributed mass and has radius \(R(R < < L)\). A star outside the galaxy is orbiting the galaxy in a plane perpendicular to the galaxy and passing through centre if the time period of star is \(T\) and its distance from the galaxy's axis is \(r\), then :

359854 The following figure shows two shells of masses \(m_{1}\) and \(m_{2}\). The shells are concentric. At which point, a particle of mass \(m\) shall experience zero force?

359855 Intensity of gravitational field inside the hollow spherical shell is

359856 Assertion :
If earth were a hollow sphere, gravitational field intensity at any point inside the earth would be zero.
Reason :
Net force on a body inside the sphere is zero.

359857 A solid sphere of mass \(M\) and radius \(R\) has a spherical cavity of radius \(R / 2\) such that the centre of cavity is at a distance \(R / 2\) from the centre of the sphere. A point mass \(m\) is placed inside the cavity at a distance \(R / 4\) from the centre of sphere. The gravitational pull between the sphere and the point mass \(m\) is

359858 A very long (length \(L\)) cylindrical galaxy is made of uniformly distributed mass and has radius \(R(R < < L)\). A star outside the galaxy is orbiting the galaxy in a plane perpendicular to the galaxy and passing through centre if the time period of star is \(T\) and its distance from the galaxy's axis is \(r\), then :

359854 The following figure shows two shells of masses \(m_{1}\) and \(m_{2}\). The shells are concentric. At which point, a particle of mass \(m\) shall experience zero force?

359855 Intensity of gravitational field inside the hollow spherical shell is

359856 Assertion :
If earth were a hollow sphere, gravitational field intensity at any point inside the earth would be zero.
Reason :
Net force on a body inside the sphere is zero.

359857 A solid sphere of mass \(M\) and radius \(R\) has a spherical cavity of radius \(R / 2\) such that the centre of cavity is at a distance \(R / 2\) from the centre of the sphere. A point mass \(m\) is placed inside the cavity at a distance \(R / 4\) from the centre of sphere. The gravitational pull between the sphere and the point mass \(m\) is

359858 A very long (length \(L\)) cylindrical galaxy is made of uniformly distributed mass and has radius \(R(R < < L)\). A star outside the galaxy is orbiting the galaxy in a plane perpendicular to the galaxy and passing through centre if the time period of star is \(T\) and its distance from the galaxy's axis is \(r\), then :

359854 The following figure shows two shells of masses \(m_{1}\) and \(m_{2}\). The shells are concentric. At which point, a particle of mass \(m\) shall experience zero force?

359855 Intensity of gravitational field inside the hollow spherical shell is

359856 Assertion :
If earth were a hollow sphere, gravitational field intensity at any point inside the earth would be zero.
Reason :
Net force on a body inside the sphere is zero.

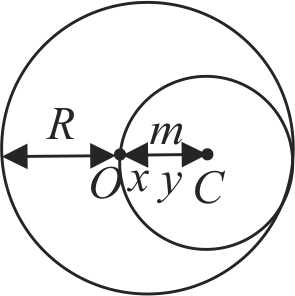
359857 A solid sphere of mass \(M\) and radius \(R\) has a spherical cavity of radius \(R / 2\) such that the centre of cavity is at a distance \(R / 2\) from the centre of the sphere. A point mass \(m\) is placed inside the cavity at a distance \(R / 4\) from the centre of sphere. The gravitational pull between the sphere and the point mass \(m\) is

359858 A very long (length \(L\)) cylindrical galaxy is made of uniformly distributed mass and has radius \(R(R < < L)\). A star outside the galaxy is orbiting the galaxy in a plane perpendicular to the galaxy and passing through centre if the time period of star is \(T\) and its distance from the galaxy's axis is \(r\), then :