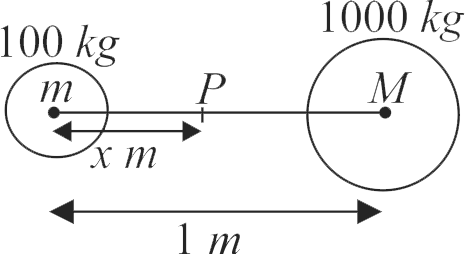
359848 At what distance (in metre) from the centre of the moon, the intensity of gravitational field will be zero? (Take, mass of earth and moon as \(5.98 \times 10^{24} \mathrm{~kg}\) and \(7.35 \times 10^{22} \mathrm{~kg}\) respectively and the distance between moon and earth is \(3.855 \times 10^{8} \mathrm{~m}\).)
359848 At what distance (in metre) from the centre of the moon, the intensity of gravitational field will be zero? (Take, mass of earth and moon as \(5.98 \times 10^{24} \mathrm{~kg}\) and \(7.35 \times 10^{22} \mathrm{~kg}\) respectively and the distance between moon and earth is \(3.855 \times 10^{8} \mathrm{~m}\).)
359848 At what distance (in metre) from the centre of the moon, the intensity of gravitational field will be zero? (Take, mass of earth and moon as \(5.98 \times 10^{24} \mathrm{~kg}\) and \(7.35 \times 10^{22} \mathrm{~kg}\) respectively and the distance between moon and earth is \(3.855 \times 10^{8} \mathrm{~m}\).)
359848 At what distance (in metre) from the centre of the moon, the intensity of gravitational field will be zero? (Take, mass of earth and moon as \(5.98 \times 10^{24} \mathrm{~kg}\) and \(7.35 \times 10^{22} \mathrm{~kg}\) respectively and the distance between moon and earth is \(3.855 \times 10^{8} \mathrm{~m}\).)