359789
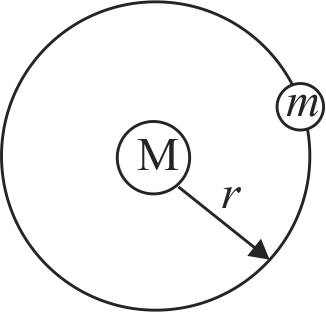
Two planets \(X\) and \(Y\) travel counter clockwise in circular orbits around a star as show in the figure below. The radii of their orbits are in the ratio \(3 \sqrt{9}: 1\). At some time, they are aligned as in fig. (\(A\)) making a straight line with the star. After five Earth years the angular displacement of planet \(X\) is \(90^{\circ}\), as in fig \(B\). What is the angular displacement of planet \(Y\) at this time?
359789
Two planets \(X\) and \(Y\) travel counter clockwise in circular orbits around a star as show in the figure below. The radii of their orbits are in the ratio \(3 \sqrt{9}: 1\). At some time, they are aligned as in fig. (\(A\)) making a straight line with the star. After five Earth years the angular displacement of planet \(X\) is \(90^{\circ}\), as in fig \(B\). What is the angular displacement of planet \(Y\) at this time?
359789
Two planets \(X\) and \(Y\) travel counter clockwise in circular orbits around a star as show in the figure below. The radii of their orbits are in the ratio \(3 \sqrt{9}: 1\). At some time, they are aligned as in fig. (\(A\)) making a straight line with the star. After five Earth years the angular displacement of planet \(X\) is \(90^{\circ}\), as in fig \(B\). What is the angular displacement of planet \(Y\) at this time?
359789
Two planets \(X\) and \(Y\) travel counter clockwise in circular orbits around a star as show in the figure below. The radii of their orbits are in the ratio \(3 \sqrt{9}: 1\). At some time, they are aligned as in fig. (\(A\)) making a straight line with the star. After five Earth years the angular displacement of planet \(X\) is \(90^{\circ}\), as in fig \(B\). What is the angular displacement of planet \(Y\) at this time?
359789
Two planets \(X\) and \(Y\) travel counter clockwise in circular orbits around a star as show in the figure below. The radii of their orbits are in the ratio \(3 \sqrt{9}: 1\). At some time, they are aligned as in fig. (\(A\)) making a straight line with the star. After five Earth years the angular displacement of planet \(X\) is \(90^{\circ}\), as in fig \(B\). What is the angular displacement of planet \(Y\) at this time?