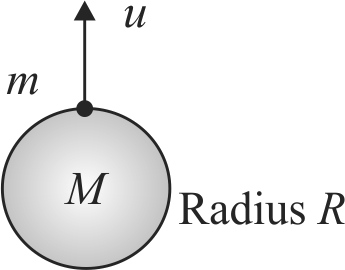
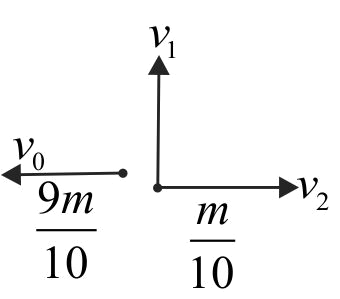
359716 A satellite of mass \(m\) is launched vertically upwards with an initial speed \(u\) from the surface of the earth. After it reaches height \(R(R = \) radius of the earth), it ejects a rocket of mass \(\dfrac{m}{10}\) so that subsequently the satellite moves in a circular orbit. The kinetic energy of the rocket is \((G\) is the gravitational constant; \(M\) is the mass of the earth) :
359718
An astronaut takes a ball of mass \(m\) from earth to space. He throws the ball into a circular orbit about earth at an altitude of \(318.5\,km\) . From earth's surface to the orbit, the change in total mechanical energy of the ball is \(x \dfrac{G M_{e} m}{21 R_{e}}\). The value of \(x\) is
(take \({R_e} = 6370\;km\) )
359716 A satellite of mass \(m\) is launched vertically upwards with an initial speed \(u\) from the surface of the earth. After it reaches height \(R(R = \) radius of the earth), it ejects a rocket of mass \(\dfrac{m}{10}\) so that subsequently the satellite moves in a circular orbit. The kinetic energy of the rocket is \((G\) is the gravitational constant; \(M\) is the mass of the earth) :
359718
An astronaut takes a ball of mass \(m\) from earth to space. He throws the ball into a circular orbit about earth at an altitude of \(318.5\,km\) . From earth's surface to the orbit, the change in total mechanical energy of the ball is \(x \dfrac{G M_{e} m}{21 R_{e}}\). The value of \(x\) is
(take \({R_e} = 6370\;km\) )
359716 A satellite of mass \(m\) is launched vertically upwards with an initial speed \(u\) from the surface of the earth. After it reaches height \(R(R = \) radius of the earth), it ejects a rocket of mass \(\dfrac{m}{10}\) so that subsequently the satellite moves in a circular orbit. The kinetic energy of the rocket is \((G\) is the gravitational constant; \(M\) is the mass of the earth) :
359718
An astronaut takes a ball of mass \(m\) from earth to space. He throws the ball into a circular orbit about earth at an altitude of \(318.5\,km\) . From earth's surface to the orbit, the change in total mechanical energy of the ball is \(x \dfrac{G M_{e} m}{21 R_{e}}\). The value of \(x\) is
(take \({R_e} = 6370\;km\) )
359716 A satellite of mass \(m\) is launched vertically upwards with an initial speed \(u\) from the surface of the earth. After it reaches height \(R(R = \) radius of the earth), it ejects a rocket of mass \(\dfrac{m}{10}\) so that subsequently the satellite moves in a circular orbit. The kinetic energy of the rocket is \((G\) is the gravitational constant; \(M\) is the mass of the earth) :
359718
An astronaut takes a ball of mass \(m\) from earth to space. He throws the ball into a circular orbit about earth at an altitude of \(318.5\,km\) . From earth's surface to the orbit, the change in total mechanical energy of the ball is \(x \dfrac{G M_{e} m}{21 R_{e}}\). The value of \(x\) is
(take \({R_e} = 6370\;km\) )