359462
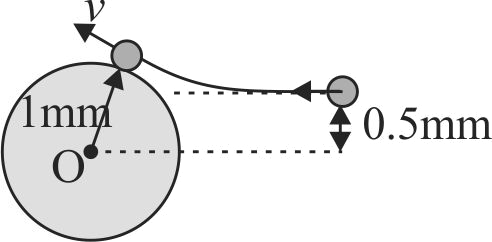
A particle of mass 1 \(kg\) & charge \(\frac{1}{3}\mu C\) is projected towards a non-conducting fixed spherical having the same charge uniformly distributed on its surface. Find the minimum initial velocity of projection required so that the particle just grazes the shell: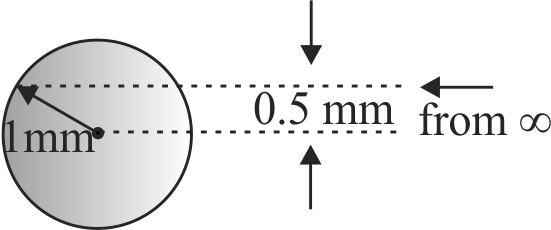
359462
A particle of mass 1 \(kg\) & charge \(\frac{1}{3}\mu C\) is projected towards a non-conducting fixed spherical having the same charge uniformly distributed on its surface. Find the minimum initial velocity of projection required so that the particle just grazes the shell:
359462
A particle of mass 1 \(kg\) & charge \(\frac{1}{3}\mu C\) is projected towards a non-conducting fixed spherical having the same charge uniformly distributed on its surface. Find the minimum initial velocity of projection required so that the particle just grazes the shell:
359462
A particle of mass 1 \(kg\) & charge \(\frac{1}{3}\mu C\) is projected towards a non-conducting fixed spherical having the same charge uniformly distributed on its surface. Find the minimum initial velocity of projection required so that the particle just grazes the shell: