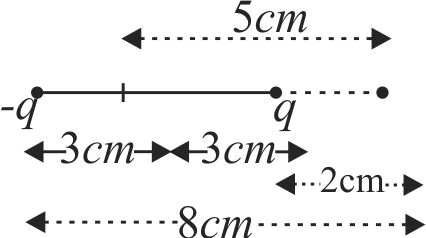359339
Read the Assertion and Reason carefully to mark the correct options given below:
Assertion :
The potential \({(V)}\) at any axial point, at \({2 m}\) distance \({(r)}\) from the centre of the dipole of dipole moment vector \({\vec{P}}\) of magnitude, \({4 \times 10^{-6} {Cm}}\), is \({\pm 9 \times 10^{3} {~V}}\).
(Take \({\dfrac{1}{4 \pi \epsilon_{0}}=9 \times 10^{9}}\) SI units)
Reason :
\({V= \pm \dfrac{2 P}{4 \pi \epsilon_{0} r^{2}}}\), where \({r}\) is the distance of any axial point, situated at \(2\,m\) from the centre of the dipole.
359339
Read the Assertion and Reason carefully to mark the correct options given below:
Assertion :
The potential \({(V)}\) at any axial point, at \({2 m}\) distance \({(r)}\) from the centre of the dipole of dipole moment vector \({\vec{P}}\) of magnitude, \({4 \times 10^{-6} {Cm}}\), is \({\pm 9 \times 10^{3} {~V}}\).
(Take \({\dfrac{1}{4 \pi \epsilon_{0}}=9 \times 10^{9}}\) SI units)
Reason :
\({V= \pm \dfrac{2 P}{4 \pi \epsilon_{0} r^{2}}}\), where \({r}\) is the distance of any axial point, situated at \(2\,m\) from the centre of the dipole.
359339
Read the Assertion and Reason carefully to mark the correct options given below:
Assertion :
The potential \({(V)}\) at any axial point, at \({2 m}\) distance \({(r)}\) from the centre of the dipole of dipole moment vector \({\vec{P}}\) of magnitude, \({4 \times 10^{-6} {Cm}}\), is \({\pm 9 \times 10^{3} {~V}}\).
(Take \({\dfrac{1}{4 \pi \epsilon_{0}}=9 \times 10^{9}}\) SI units)
Reason :
\({V= \pm \dfrac{2 P}{4 \pi \epsilon_{0} r^{2}}}\), where \({r}\) is the distance of any axial point, situated at \(2\,m\) from the centre of the dipole.
359339
Read the Assertion and Reason carefully to mark the correct options given below:
Assertion :
The potential \({(V)}\) at any axial point, at \({2 m}\) distance \({(r)}\) from the centre of the dipole of dipole moment vector \({\vec{P}}\) of magnitude, \({4 \times 10^{-6} {Cm}}\), is \({\pm 9 \times 10^{3} {~V}}\).
(Take \({\dfrac{1}{4 \pi \epsilon_{0}}=9 \times 10^{9}}\) SI units)
Reason :
\({V= \pm \dfrac{2 P}{4 \pi \epsilon_{0} r^{2}}}\), where \({r}\) is the distance of any axial point, situated at \(2\,m\) from the centre of the dipole.