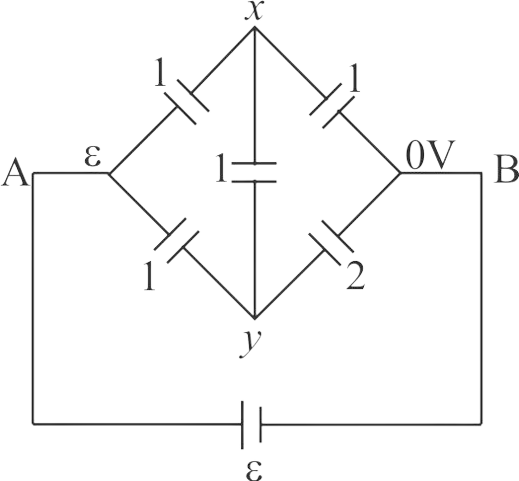
Explanation:
The given circuit is not a wheatstone bridge. To find equivalent capacitance we assume a battery connected between \(A\) and \(B\). Let the potential of (+) ve terminal be \(\varepsilon \) and that of \(( - ve)\) terminal be 0 \(V\). Let \(x\) and \(y\) be potentials at the two junctions
From the junction rule
\(x = \frac{{1\left( \varepsilon \right) + 1\left( y \right) + 1\left( 0 \right)}}{{1 + 1 + 1}} = \frac{{\varepsilon + y}}{3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\)
\(y = \frac{{1\left( \varepsilon \right) + 1\left( x \right) + 2\left( 0 \right)}}{{1 + 1 + 2}} = \frac{{\varepsilon + x}}{4}\,\,\,\,\,\,\,\,\,\,\,\,\,(2)\)
From Eq’s (1) & (2) we get
\(x = \frac{{5\varepsilon }}{{11}}\,\,\& y = \frac{{4\varepsilon }}{{11}}\)
The equivalent capacitance is \({C_{eq}} = \frac{q}{\varepsilon }\)
Where \(q\) is the total (+) ve charge supplied by the battery.
\(q = 1\mu F\left( {\varepsilon - x} \right) + 1\mu F\left( {\varepsilon - y} \right) = \frac{{13\varepsilon }}{{11}}\)
\({C_{eq}} = \frac{q}{\varepsilon } = \frac{{13}}{{11}}\mu F\)