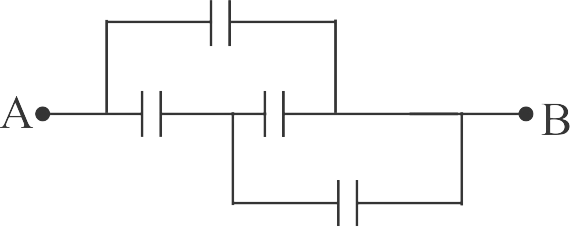
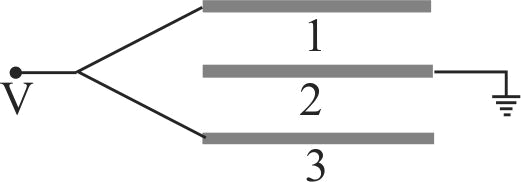
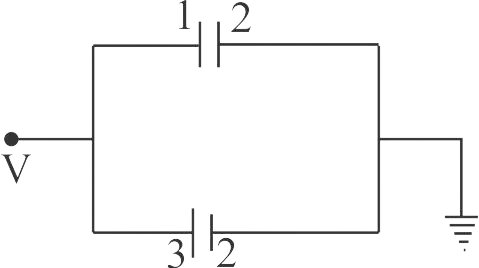
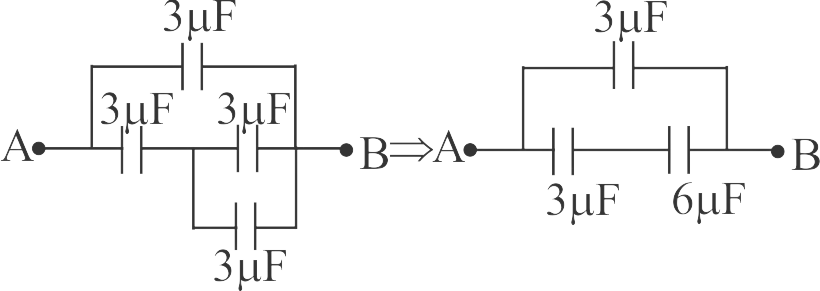359264 A series combination of \(n_{1}\) capacitors, each of value \(C_{1}\) is charges by a source of potential difference \(4 V\). When another parallel combination of \(n_{2}\) capacitors, each of value \(C_{2}\) is charges by a source of potential difference \(V\), it has the same (total) energy stored in it, as the first combination has. The value of \(C_{2}\), in terms of \(C_{1}\) is, then:
359264 A series combination of \(n_{1}\) capacitors, each of value \(C_{1}\) is charges by a source of potential difference \(4 V\). When another parallel combination of \(n_{2}\) capacitors, each of value \(C_{2}\) is charges by a source of potential difference \(V\), it has the same (total) energy stored in it, as the first combination has. The value of \(C_{2}\), in terms of \(C_{1}\) is, then:
359264 A series combination of \(n_{1}\) capacitors, each of value \(C_{1}\) is charges by a source of potential difference \(4 V\). When another parallel combination of \(n_{2}\) capacitors, each of value \(C_{2}\) is charges by a source of potential difference \(V\), it has the same (total) energy stored in it, as the first combination has. The value of \(C_{2}\), in terms of \(C_{1}\) is, then:
359264 A series combination of \(n_{1}\) capacitors, each of value \(C_{1}\) is charges by a source of potential difference \(4 V\). When another parallel combination of \(n_{2}\) capacitors, each of value \(C_{2}\) is charges by a source of potential difference \(V\), it has the same (total) energy stored in it, as the first combination has. The value of \(C_{2}\), in terms of \(C_{1}\) is, then: