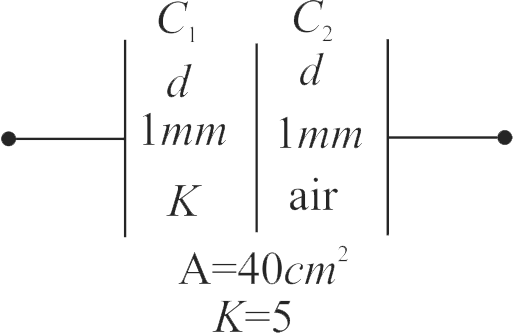359228
The space between the plates of a parallel plate capacitor is filled with
359228
The space between the plates of a parallel plate capacitor is filled with
359228
The space between the plates of a parallel plate capacitor is filled with
359228
The space between the plates of a parallel plate capacitor is filled with
359228
The space between the plates of a parallel plate capacitor is filled with