359186
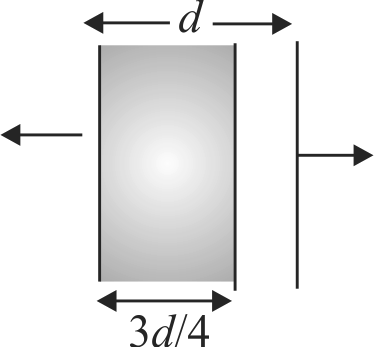
A combination of parallel plate capacitors is maintained at a certain potential difference. When a 3 \(mm\) thick slab is introduced between all the plates, in order to maintain the same potential difference, the distance between plates in increased by 2.4 \(mm\). Find the dielectric constant of the slab.
359188
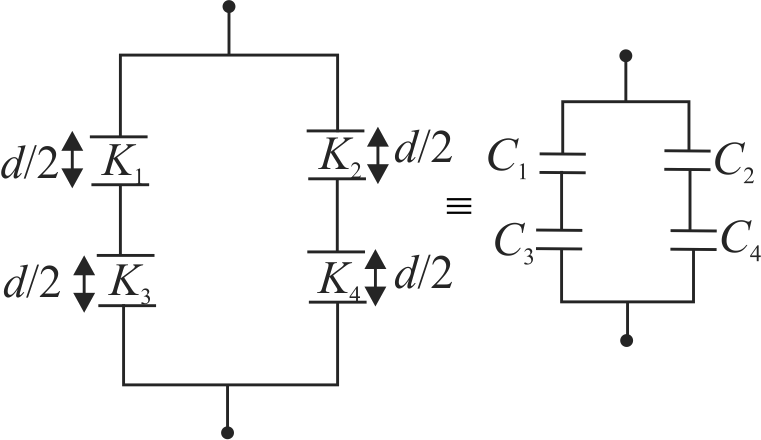
A parallel plate capacitor of area \(A\), plate separation \(d\) and capacitance \(C\) is filled with three different dielectric material having dielectric constants \({K_1},{K_2}\) and \({K_3}\) as shown. If a single dielectric material is to be used to have the same capacitance \(C\) in this capacitor, then its dielectric constant \(k\) is given by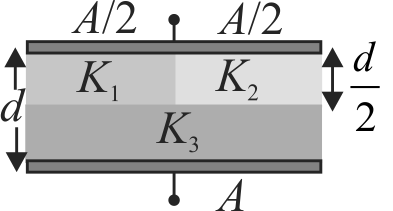
359186
A combination of parallel plate capacitors is maintained at a certain potential difference. When a 3 \(mm\) thick slab is introduced between all the plates, in order to maintain the same potential difference, the distance between plates in increased by 2.4 \(mm\). Find the dielectric constant of the slab.
359188
A parallel plate capacitor of area \(A\), plate separation \(d\) and capacitance \(C\) is filled with three different dielectric material having dielectric constants \({K_1},{K_2}\) and \({K_3}\) as shown. If a single dielectric material is to be used to have the same capacitance \(C\) in this capacitor, then its dielectric constant \(k\) is given by
359186
A combination of parallel plate capacitors is maintained at a certain potential difference. When a 3 \(mm\) thick slab is introduced between all the plates, in order to maintain the same potential difference, the distance between plates in increased by 2.4 \(mm\). Find the dielectric constant of the slab.
359188
A parallel plate capacitor of area \(A\), plate separation \(d\) and capacitance \(C\) is filled with three different dielectric material having dielectric constants \({K_1},{K_2}\) and \({K_3}\) as shown. If a single dielectric material is to be used to have the same capacitance \(C\) in this capacitor, then its dielectric constant \(k\) is given by
359186
A combination of parallel plate capacitors is maintained at a certain potential difference. When a 3 \(mm\) thick slab is introduced between all the plates, in order to maintain the same potential difference, the distance between plates in increased by 2.4 \(mm\). Find the dielectric constant of the slab.
359188
A parallel plate capacitor of area \(A\), plate separation \(d\) and capacitance \(C\) is filled with three different dielectric material having dielectric constants \({K_1},{K_2}\) and \({K_3}\) as shown. If a single dielectric material is to be used to have the same capacitance \(C\) in this capacitor, then its dielectric constant \(k\) is given by