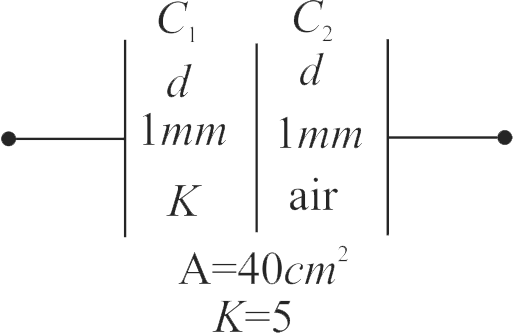359224
Consider a parallel plate capacitor of capacity \(10\mu F\) filled with air. When the gap between the plate is filled partly with a dielectric of dielectric constant 4, as shown in figure. The new capacity of the capacitor is (A is the area of plates)
359228 The space between the plates of a parallel plate capacitor is filled with \(a\) ‘dielectric’ whose ‘dielectric constant’ varies with distance as per the relation :\(K({\rm{x}}) = {K_o} + \lambda {\rm{x}}\) \((\lambda \)= a constant ) The capacitance \(C\), of this capacitor, would be related to its ‘vacuum’ capacitance \({C_0}\) as per the relation (\(d\) is the separation between the plates)
359224
Consider a parallel plate capacitor of capacity \(10\mu F\) filled with air. When the gap between the plate is filled partly with a dielectric of dielectric constant 4, as shown in figure. The new capacity of the capacitor is (A is the area of plates)
359228 The space between the plates of a parallel plate capacitor is filled with \(a\) ‘dielectric’ whose ‘dielectric constant’ varies with distance as per the relation :\(K({\rm{x}}) = {K_o} + \lambda {\rm{x}}\) \((\lambda \)= a constant ) The capacitance \(C\), of this capacitor, would be related to its ‘vacuum’ capacitance \({C_0}\) as per the relation (\(d\) is the separation between the plates)
359224
Consider a parallel plate capacitor of capacity \(10\mu F\) filled with air. When the gap between the plate is filled partly with a dielectric of dielectric constant 4, as shown in figure. The new capacity of the capacitor is (A is the area of plates)
359228 The space between the plates of a parallel plate capacitor is filled with \(a\) ‘dielectric’ whose ‘dielectric constant’ varies with distance as per the relation :\(K({\rm{x}}) = {K_o} + \lambda {\rm{x}}\) \((\lambda \)= a constant ) The capacitance \(C\), of this capacitor, would be related to its ‘vacuum’ capacitance \({C_0}\) as per the relation (\(d\) is the separation between the plates)
359224
Consider a parallel plate capacitor of capacity \(10\mu F\) filled with air. When the gap between the plate is filled partly with a dielectric of dielectric constant 4, as shown in figure. The new capacity of the capacitor is (A is the area of plates)
359228 The space between the plates of a parallel plate capacitor is filled with \(a\) ‘dielectric’ whose ‘dielectric constant’ varies with distance as per the relation :\(K({\rm{x}}) = {K_o} + \lambda {\rm{x}}\) \((\lambda \)= a constant ) The capacitance \(C\), of this capacitor, would be related to its ‘vacuum’ capacitance \({C_0}\) as per the relation (\(d\) is the separation between the plates)
359224
Consider a parallel plate capacitor of capacity \(10\mu F\) filled with air. When the gap between the plate is filled partly with a dielectric of dielectric constant 4, as shown in figure. The new capacity of the capacitor is (A is the area of plates)
359228 The space between the plates of a parallel plate capacitor is filled with \(a\) ‘dielectric’ whose ‘dielectric constant’ varies with distance as per the relation :\(K({\rm{x}}) = {K_o} + \lambda {\rm{x}}\) \((\lambda \)= a constant ) The capacitance \(C\), of this capacitor, would be related to its ‘vacuum’ capacitance \({C_0}\) as per the relation (\(d\) is the separation between the plates)