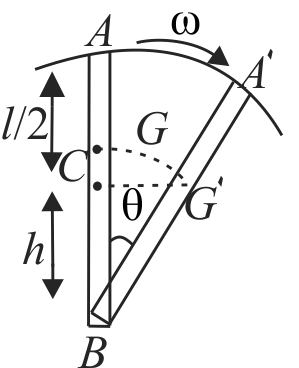366277
Two uniform discs of equal mass but unequal radii are mounted on fixed horizontal axiles. Light strings are wrapped on each of the discs. The strings are pulled by constant equal forces \(\mathrm{F}\) for same amount of time as shown in the figure.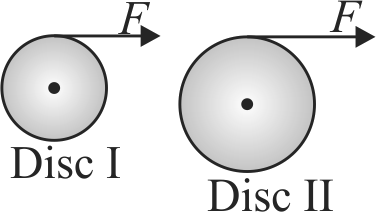
366279 A cord is wound round the circumference of wheel of radius \(r\). The axis of the wheel is horizontal and moment of inertia about it is \(I.{\rm{ }}A\) weight \(mg\) is attached to the end of the cord and falls from the rest. After falling through a distance \(h\), the angular velocity of the wheel will be
366280
A uniform rod of length \(l\) is free to rotate in a vertical plane about a fixed horizontal axis through \(B\). The rod begins rotating from rest from its unstable equilibrium position. When it has turned through an angle \(\theta\), its angular velocity \(\omega\) is given by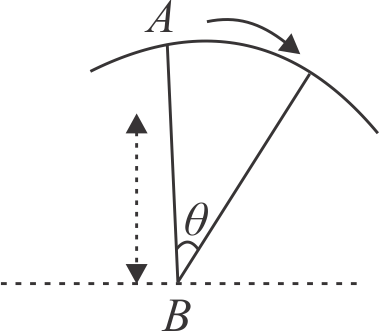
366277
Two uniform discs of equal mass but unequal radii are mounted on fixed horizontal axiles. Light strings are wrapped on each of the discs. The strings are pulled by constant equal forces \(\mathrm{F}\) for same amount of time as shown in the figure.
366279 A cord is wound round the circumference of wheel of radius \(r\). The axis of the wheel is horizontal and moment of inertia about it is \(I.{\rm{ }}A\) weight \(mg\) is attached to the end of the cord and falls from the rest. After falling through a distance \(h\), the angular velocity of the wheel will be
366280
A uniform rod of length \(l\) is free to rotate in a vertical plane about a fixed horizontal axis through \(B\). The rod begins rotating from rest from its unstable equilibrium position. When it has turned through an angle \(\theta\), its angular velocity \(\omega\) is given by
366277
Two uniform discs of equal mass but unequal radii are mounted on fixed horizontal axiles. Light strings are wrapped on each of the discs. The strings are pulled by constant equal forces \(\mathrm{F}\) for same amount of time as shown in the figure.
366279 A cord is wound round the circumference of wheel of radius \(r\). The axis of the wheel is horizontal and moment of inertia about it is \(I.{\rm{ }}A\) weight \(mg\) is attached to the end of the cord and falls from the rest. After falling through a distance \(h\), the angular velocity of the wheel will be
366280
A uniform rod of length \(l\) is free to rotate in a vertical plane about a fixed horizontal axis through \(B\). The rod begins rotating from rest from its unstable equilibrium position. When it has turned through an angle \(\theta\), its angular velocity \(\omega\) is given by
366277
Two uniform discs of equal mass but unequal radii are mounted on fixed horizontal axiles. Light strings are wrapped on each of the discs. The strings are pulled by constant equal forces \(\mathrm{F}\) for same amount of time as shown in the figure.
366279 A cord is wound round the circumference of wheel of radius \(r\). The axis of the wheel is horizontal and moment of inertia about it is \(I.{\rm{ }}A\) weight \(mg\) is attached to the end of the cord and falls from the rest. After falling through a distance \(h\), the angular velocity of the wheel will be
366280
A uniform rod of length \(l\) is free to rotate in a vertical plane about a fixed horizontal axis through \(B\). The rod begins rotating from rest from its unstable equilibrium position. When it has turned through an angle \(\theta\), its angular velocity \(\omega\) is given by
366277
Two uniform discs of equal mass but unequal radii are mounted on fixed horizontal axiles. Light strings are wrapped on each of the discs. The strings are pulled by constant equal forces \(\mathrm{F}\) for same amount of time as shown in the figure.
366279 A cord is wound round the circumference of wheel of radius \(r\). The axis of the wheel is horizontal and moment of inertia about it is \(I.{\rm{ }}A\) weight \(mg\) is attached to the end of the cord and falls from the rest. After falling through a distance \(h\), the angular velocity of the wheel will be
366280
A uniform rod of length \(l\) is free to rotate in a vertical plane about a fixed horizontal axis through \(B\). The rod begins rotating from rest from its unstable equilibrium position. When it has turned through an angle \(\theta\), its angular velocity \(\omega\) is given by