366217 Figure shows a uniform block of mass \({m=\sqrt{\dfrac{3}{13}} {~kg}}\) having square base and equilateral triangular cross section placed at the edge of the floor of a truck which is under constant acceleration \({a=\dfrac{g \sqrt{3}}{4} {~m} / {s}^{2}}\) to the right. A horizontal force on the apex of the triangle \({F}\) is just enough to just tilt the block. Find the force on the block at point \({A}\) where the block is in contact with the step edge when \({F}\) is applied. (Take \({g=10 {~m} / {s}^{2}}\))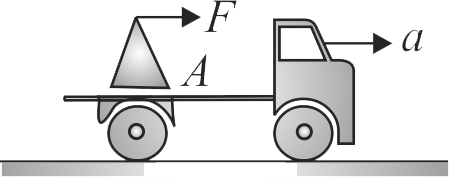

366218 A cube of side \(a\) is placed on an inclined plane of inclination \(\theta\). What is the maximum value of \(\theta\) for which the cube will not topple?

366219 Calculate the force \(F\) that is applied horizontally at the axle of the wheel which is necessary to raise the wheel over the obstacle of height \(0.4\,\,m\). Radius of wheel is \(1\,\;m\) and mass \( = 10\;kg\). \(F\) is

366220 A cube of side \(a\) and mass \(m\) is to be tilted at point \(A\) by applying a force \(F\) as shown in figure. The minimum force required is

366217 Figure shows a uniform block of mass \({m=\sqrt{\dfrac{3}{13}} {~kg}}\) having square base and equilateral triangular cross section placed at the edge of the floor of a truck which is under constant acceleration \({a=\dfrac{g \sqrt{3}}{4} {~m} / {s}^{2}}\) to the right. A horizontal force on the apex of the triangle \({F}\) is just enough to just tilt the block. Find the force on the block at point \({A}\) where the block is in contact with the step edge when \({F}\) is applied. (Take \({g=10 {~m} / {s}^{2}}\))

366218 A cube of side \(a\) is placed on an inclined plane of inclination \(\theta\). What is the maximum value of \(\theta\) for which the cube will not topple?

366219 Calculate the force \(F\) that is applied horizontally at the axle of the wheel which is necessary to raise the wheel over the obstacle of height \(0.4\,\,m\). Radius of wheel is \(1\,\;m\) and mass \( = 10\;kg\). \(F\) is

366220 A cube of side \(a\) and mass \(m\) is to be tilted at point \(A\) by applying a force \(F\) as shown in figure. The minimum force required is

366217 Figure shows a uniform block of mass \({m=\sqrt{\dfrac{3}{13}} {~kg}}\) having square base and equilateral triangular cross section placed at the edge of the floor of a truck which is under constant acceleration \({a=\dfrac{g \sqrt{3}}{4} {~m} / {s}^{2}}\) to the right. A horizontal force on the apex of the triangle \({F}\) is just enough to just tilt the block. Find the force on the block at point \({A}\) where the block is in contact with the step edge when \({F}\) is applied. (Take \({g=10 {~m} / {s}^{2}}\))

366218 A cube of side \(a\) is placed on an inclined plane of inclination \(\theta\). What is the maximum value of \(\theta\) for which the cube will not topple?

366219 Calculate the force \(F\) that is applied horizontally at the axle of the wheel which is necessary to raise the wheel over the obstacle of height \(0.4\,\,m\). Radius of wheel is \(1\,\;m\) and mass \( = 10\;kg\). \(F\) is

366220 A cube of side \(a\) and mass \(m\) is to be tilted at point \(A\) by applying a force \(F\) as shown in figure. The minimum force required is

366217 Figure shows a uniform block of mass \({m=\sqrt{\dfrac{3}{13}} {~kg}}\) having square base and equilateral triangular cross section placed at the edge of the floor of a truck which is under constant acceleration \({a=\dfrac{g \sqrt{3}}{4} {~m} / {s}^{2}}\) to the right. A horizontal force on the apex of the triangle \({F}\) is just enough to just tilt the block. Find the force on the block at point \({A}\) where the block is in contact with the step edge when \({F}\) is applied. (Take \({g=10 {~m} / {s}^{2}}\))

366218 A cube of side \(a\) is placed on an inclined plane of inclination \(\theta\). What is the maximum value of \(\theta\) for which the cube will not topple?

366219 Calculate the force \(F\) that is applied horizontally at the axle of the wheel which is necessary to raise the wheel over the obstacle of height \(0.4\,\,m\). Radius of wheel is \(1\,\;m\) and mass \( = 10\;kg\). \(F\) is

366220 A cube of side \(a\) and mass \(m\) is to be tilted at point \(A\) by applying a force \(F\) as shown in figure. The minimum force required is