366170 A particle of mass \(m\) is moving in \(y z\) - plane with a uniform velocity \(v\) with its trajectory running parallel to +ve \(y\)-axis and intersecting z-axis at \(z = a\). The change in its angular momentum about the origin as it bounces elastically from a wall at \(y = \) constant is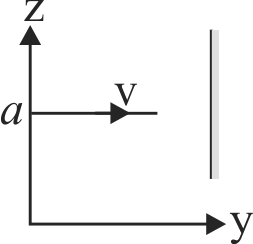

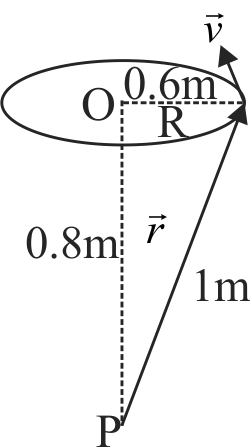
366171 The moment of momentum is called

366172 A particle of mass \(m\) in the \(XY\)-plane with a velocity \(v\) along the straight line \(AB\). If the angular momentum of the particle with respect to orgin \(O\) is \(L_{A}\) when it is at \(A\) and \(L_{B}\) when it is at \(B\), then

366173 A particle of mass \(2 \mathrm{~kg}\) is on a smooth horizontal table and moves in a circular path of radius 0.6 \(\mathrm{m}\). The height of the table from the ground is 0.8 . If the angular speed of the particle is \(12 \mathrm{rad} \mathrm{s}^{-1}\), the magnitude of its angular omentum about a point on the ground right under the centre of the circle is:

366170 A particle of mass \(m\) is moving in \(y z\) - plane with a uniform velocity \(v\) with its trajectory running parallel to +ve \(y\)-axis and intersecting z-axis at \(z = a\). The change in its angular momentum about the origin as it bounces elastically from a wall at \(y = \) constant is

366171 The moment of momentum is called

366172 A particle of mass \(m\) in the \(XY\)-plane with a velocity \(v\) along the straight line \(AB\). If the angular momentum of the particle with respect to orgin \(O\) is \(L_{A}\) when it is at \(A\) and \(L_{B}\) when it is at \(B\), then

366173 A particle of mass \(2 \mathrm{~kg}\) is on a smooth horizontal table and moves in a circular path of radius 0.6 \(\mathrm{m}\). The height of the table from the ground is 0.8 . If the angular speed of the particle is \(12 \mathrm{rad} \mathrm{s}^{-1}\), the magnitude of its angular omentum about a point on the ground right under the centre of the circle is:

366170 A particle of mass \(m\) is moving in \(y z\) - plane with a uniform velocity \(v\) with its trajectory running parallel to +ve \(y\)-axis and intersecting z-axis at \(z = a\). The change in its angular momentum about the origin as it bounces elastically from a wall at \(y = \) constant is

366171 The moment of momentum is called

366172 A particle of mass \(m\) in the \(XY\)-plane with a velocity \(v\) along the straight line \(AB\). If the angular momentum of the particle with respect to orgin \(O\) is \(L_{A}\) when it is at \(A\) and \(L_{B}\) when it is at \(B\), then

366173 A particle of mass \(2 \mathrm{~kg}\) is on a smooth horizontal table and moves in a circular path of radius 0.6 \(\mathrm{m}\). The height of the table from the ground is 0.8 . If the angular speed of the particle is \(12 \mathrm{rad} \mathrm{s}^{-1}\), the magnitude of its angular omentum about a point on the ground right under the centre of the circle is:

366170 A particle of mass \(m\) is moving in \(y z\) - plane with a uniform velocity \(v\) with its trajectory running parallel to +ve \(y\)-axis and intersecting z-axis at \(z = a\). The change in its angular momentum about the origin as it bounces elastically from a wall at \(y = \) constant is

366171 The moment of momentum is called

366172 A particle of mass \(m\) in the \(XY\)-plane with a velocity \(v\) along the straight line \(AB\). If the angular momentum of the particle with respect to orgin \(O\) is \(L_{A}\) when it is at \(A\) and \(L_{B}\) when it is at \(B\), then

366173 A particle of mass \(2 \mathrm{~kg}\) is on a smooth horizontal table and moves in a circular path of radius 0.6 \(\mathrm{m}\). The height of the table from the ground is 0.8 . If the angular speed of the particle is \(12 \mathrm{rad} \mathrm{s}^{-1}\), the magnitude of its angular omentum about a point on the ground right under the centre of the circle is: