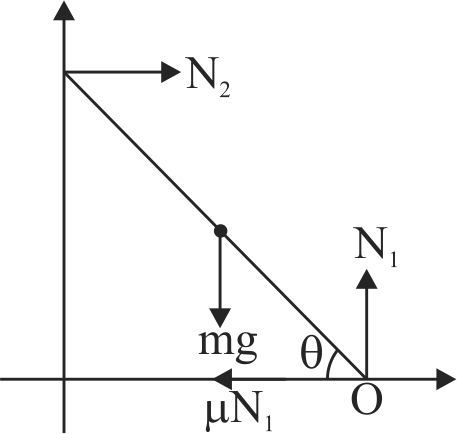
366157 A ladder of length \(l\) and mass \(m\) is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is \(\mu\). The angle \(\theta\) at which the ladder will stay in equilibrium is

366158 A particle of mass \(5\;g\) is moving with a uniform speed of \(3\sqrt 2 \;cm/s\) in the \(x-y\) plane along the line \(y=x+4\). The magnitude of its angular momentum about the origin in \(gc{m^2}/s\) is :

366159 The position of a particle is given by: \(\vec{r}=(\hat{i}+2 \hat{j}-\hat{k})\) and momentum \(\vec{P}=(3 \hat{i}+4 \hat{j}-2 \hat{k})\). The angular momentum is perpendicular to

366160 Angular momentum \(L\) of body with moment of inertia I and angular velocity \(\omega \,\,rad/\sec \) is equal to

366157 A ladder of length \(l\) and mass \(m\) is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is \(\mu\). The angle \(\theta\) at which the ladder will stay in equilibrium is

366158 A particle of mass \(5\;g\) is moving with a uniform speed of \(3\sqrt 2 \;cm/s\) in the \(x-y\) plane along the line \(y=x+4\). The magnitude of its angular momentum about the origin in \(gc{m^2}/s\) is :

366159 The position of a particle is given by: \(\vec{r}=(\hat{i}+2 \hat{j}-\hat{k})\) and momentum \(\vec{P}=(3 \hat{i}+4 \hat{j}-2 \hat{k})\). The angular momentum is perpendicular to

366160 Angular momentum \(L\) of body with moment of inertia I and angular velocity \(\omega \,\,rad/\sec \) is equal to

366157 A ladder of length \(l\) and mass \(m\) is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is \(\mu\). The angle \(\theta\) at which the ladder will stay in equilibrium is

366158 A particle of mass \(5\;g\) is moving with a uniform speed of \(3\sqrt 2 \;cm/s\) in the \(x-y\) plane along the line \(y=x+4\). The magnitude of its angular momentum about the origin in \(gc{m^2}/s\) is :

366159 The position of a particle is given by: \(\vec{r}=(\hat{i}+2 \hat{j}-\hat{k})\) and momentum \(\vec{P}=(3 \hat{i}+4 \hat{j}-2 \hat{k})\). The angular momentum is perpendicular to

366160 Angular momentum \(L\) of body with moment of inertia I and angular velocity \(\omega \,\,rad/\sec \) is equal to

366157 A ladder of length \(l\) and mass \(m\) is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is \(\mu\). The angle \(\theta\) at which the ladder will stay in equilibrium is

366158 A particle of mass \(5\;g\) is moving with a uniform speed of \(3\sqrt 2 \;cm/s\) in the \(x-y\) plane along the line \(y=x+4\). The magnitude of its angular momentum about the origin in \(gc{m^2}/s\) is :

366159 The position of a particle is given by: \(\vec{r}=(\hat{i}+2 \hat{j}-\hat{k})\) and momentum \(\vec{P}=(3 \hat{i}+4 \hat{j}-2 \hat{k})\). The angular momentum is perpendicular to

366160 Angular momentum \(L\) of body with moment of inertia I and angular velocity \(\omega \,\,rad/\sec \) is equal to