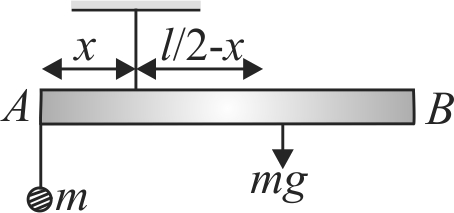
366136 A uniform \(\operatorname{rod} A B\) is suspended from a point \(X\), at a variable distance \(x\) from \(\mathrm{A}\), as shown. To make the rod horizontal, a mass \(m\) is suspended from its end A. A set of \((m, x)\) values is recorded. The appropriate variables that give a straight line, when plotted, are:

366137 If a street light of mass \(M\) is suspended from the end of a uniform rod of length \(l\) in different possible patterns as shown in figure, then:

366138 Two rods each of mass \({m=4 {~kg}}\) and length \({l=1 {~m}}\) are in equilibrium being smoothly hinged at \({P}\). The tension in the connecting string as shown in figure is

366139 A uniform cube of mass \(M\) and side \(a\) is placed on a frictionless horizontal surface. A vertical force \(F\) is applied to edge as shown in figure. If \(F=\dfrac{M g}{4}\) then find the distance of normal force line from point \(O\).

366136 A uniform \(\operatorname{rod} A B\) is suspended from a point \(X\), at a variable distance \(x\) from \(\mathrm{A}\), as shown. To make the rod horizontal, a mass \(m\) is suspended from its end A. A set of \((m, x)\) values is recorded. The appropriate variables that give a straight line, when plotted, are:

366137 If a street light of mass \(M\) is suspended from the end of a uniform rod of length \(l\) in different possible patterns as shown in figure, then:

366138 Two rods each of mass \({m=4 {~kg}}\) and length \({l=1 {~m}}\) are in equilibrium being smoothly hinged at \({P}\). The tension in the connecting string as shown in figure is

366139 A uniform cube of mass \(M\) and side \(a\) is placed on a frictionless horizontal surface. A vertical force \(F\) is applied to edge as shown in figure. If \(F=\dfrac{M g}{4}\) then find the distance of normal force line from point \(O\).

366136 A uniform \(\operatorname{rod} A B\) is suspended from a point \(X\), at a variable distance \(x\) from \(\mathrm{A}\), as shown. To make the rod horizontal, a mass \(m\) is suspended from its end A. A set of \((m, x)\) values is recorded. The appropriate variables that give a straight line, when plotted, are:

366137 If a street light of mass \(M\) is suspended from the end of a uniform rod of length \(l\) in different possible patterns as shown in figure, then:

366138 Two rods each of mass \({m=4 {~kg}}\) and length \({l=1 {~m}}\) are in equilibrium being smoothly hinged at \({P}\). The tension in the connecting string as shown in figure is

366139 A uniform cube of mass \(M\) and side \(a\) is placed on a frictionless horizontal surface. A vertical force \(F\) is applied to edge as shown in figure. If \(F=\dfrac{M g}{4}\) then find the distance of normal force line from point \(O\).

366136 A uniform \(\operatorname{rod} A B\) is suspended from a point \(X\), at a variable distance \(x\) from \(\mathrm{A}\), as shown. To make the rod horizontal, a mass \(m\) is suspended from its end A. A set of \((m, x)\) values is recorded. The appropriate variables that give a straight line, when plotted, are:

366137 If a street light of mass \(M\) is suspended from the end of a uniform rod of length \(l\) in different possible patterns as shown in figure, then:

366138 Two rods each of mass \({m=4 {~kg}}\) and length \({l=1 {~m}}\) are in equilibrium being smoothly hinged at \({P}\). The tension in the connecting string as shown in figure is

366139 A uniform cube of mass \(M\) and side \(a\) is placed on a frictionless horizontal surface. A vertical force \(F\) is applied to edge as shown in figure. If \(F=\dfrac{M g}{4}\) then find the distance of normal force line from point \(O\).