366073
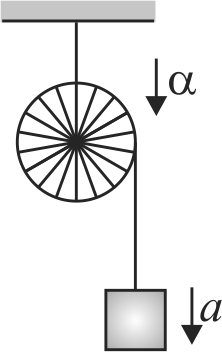
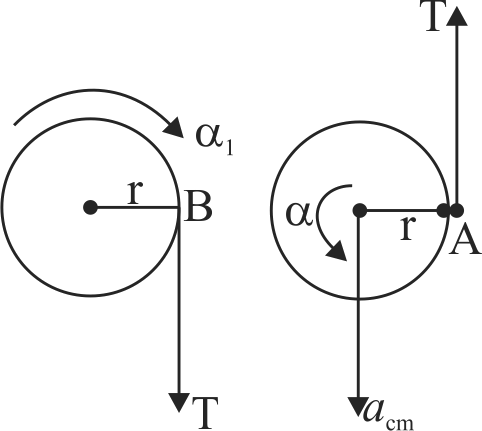
Two identical uniform discs of mass \(m\) and radius \(\mathrm{r}\) are arranged as shown in the figure. If \(\alpha\) is the angular acceleration of the lower disc and \(a_{c m}\) is acceleration of centre of mass of the lower disc, then relation among \(a_{c m}, \alpha\) and \(\mathrm{r}\) is: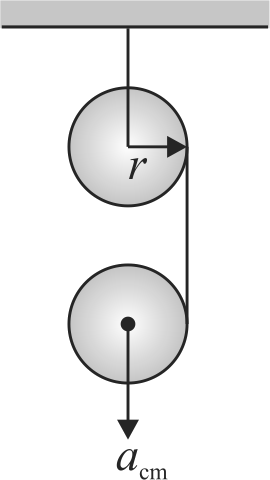
366073
Two identical uniform discs of mass \(m\) and radius \(\mathrm{r}\) are arranged as shown in the figure. If \(\alpha\) is the angular acceleration of the lower disc and \(a_{c m}\) is acceleration of centre of mass of the lower disc, then relation among \(a_{c m}, \alpha\) and \(\mathrm{r}\) is:
366073
Two identical uniform discs of mass \(m\) and radius \(\mathrm{r}\) are arranged as shown in the figure. If \(\alpha\) is the angular acceleration of the lower disc and \(a_{c m}\) is acceleration of centre of mass of the lower disc, then relation among \(a_{c m}, \alpha\) and \(\mathrm{r}\) is: