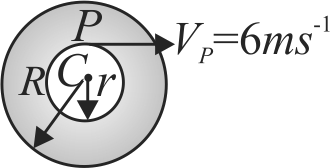366054
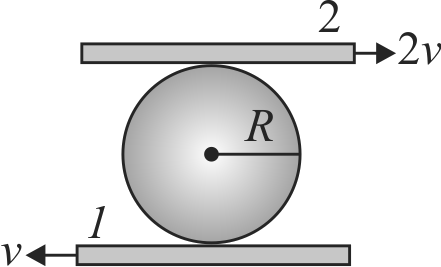
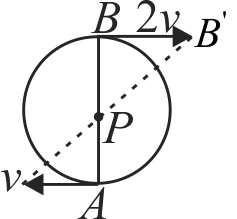
A sphere is rolling without slipping on a fixed horizonal plane surface. In the figure, \(\mathrm{A}\) is the point of contanct, \(\mathrm{B}\) is the center of the sphere and \(\mathrm{C}\) is its topmost point. Then:
(i) \({\overrightarrow V _C} - {\overrightarrow V _A} = 2\left( {{{\overrightarrow V }_B} - {{\overrightarrow V }_C}} \right)\)
(ii) \({\overrightarrow V _C} - {\overrightarrow V _B} = {\overrightarrow V _B} - {\overrightarrow V _A}\)
(iii) \(\left| {{{\overrightarrow V }_C} - {{\overrightarrow V }_A}} \right| = 2\left| {{{\overrightarrow V }_B} - {{\overrightarrow V }_C}} \right|\)
(iv) \(\left| {{{\overrightarrow V }_C} - {{\overrightarrow V }_A}} \right| = 4\left| {{{\overrightarrow V }_B}} \right|\)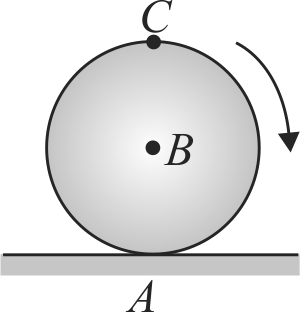
366054
A sphere is rolling without slipping on a fixed horizonal plane surface. In the figure, \(\mathrm{A}\) is the point of contanct, \(\mathrm{B}\) is the center of the sphere and \(\mathrm{C}\) is its topmost point. Then:
(i) \({\overrightarrow V _C} - {\overrightarrow V _A} = 2\left( {{{\overrightarrow V }_B} - {{\overrightarrow V }_C}} \right)\)
(ii) \({\overrightarrow V _C} - {\overrightarrow V _B} = {\overrightarrow V _B} - {\overrightarrow V _A}\)
(iii) \(\left| {{{\overrightarrow V }_C} - {{\overrightarrow V }_A}} \right| = 2\left| {{{\overrightarrow V }_B} - {{\overrightarrow V }_C}} \right|\)
(iv) \(\left| {{{\overrightarrow V }_C} - {{\overrightarrow V }_A}} \right| = 4\left| {{{\overrightarrow V }_B}} \right|\)
366054
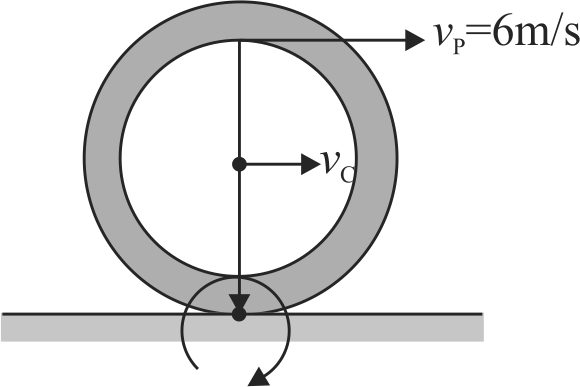
A sphere is rolling without slipping on a fixed horizonal plane surface. In the figure, \(\mathrm{A}\) is the point of contanct, \(\mathrm{B}\) is the center of the sphere and \(\mathrm{C}\) is its topmost point. Then:
(i) \({\overrightarrow V _C} - {\overrightarrow V _A} = 2\left( {{{\overrightarrow V }_B} - {{\overrightarrow V }_C}} \right)\)
(ii) \({\overrightarrow V _C} - {\overrightarrow V _B} = {\overrightarrow V _B} - {\overrightarrow V _A}\)
(iii) \(\left| {{{\overrightarrow V }_C} - {{\overrightarrow V }_A}} \right| = 2\left| {{{\overrightarrow V }_B} - {{\overrightarrow V }_C}} \right|\)
(iv) \(\left| {{{\overrightarrow V }_C} - {{\overrightarrow V }_A}} \right| = 4\left| {{{\overrightarrow V }_B}} \right|\)
366054
A sphere is rolling without slipping on a fixed horizonal plane surface. In the figure, \(\mathrm{A}\) is the point of contanct, \(\mathrm{B}\) is the center of the sphere and \(\mathrm{C}\) is its topmost point. Then:
(i) \({\overrightarrow V _C} - {\overrightarrow V _A} = 2\left( {{{\overrightarrow V }_B} - {{\overrightarrow V }_C}} \right)\)
(ii) \({\overrightarrow V _C} - {\overrightarrow V _B} = {\overrightarrow V _B} - {\overrightarrow V _A}\)
(iii) \(\left| {{{\overrightarrow V }_C} - {{\overrightarrow V }_A}} \right| = 2\left| {{{\overrightarrow V }_B} - {{\overrightarrow V }_C}} \right|\)
(iv) \(\left| {{{\overrightarrow V }_C} - {{\overrightarrow V }_A}} \right| = 4\left| {{{\overrightarrow V }_B}} \right|\)