366050
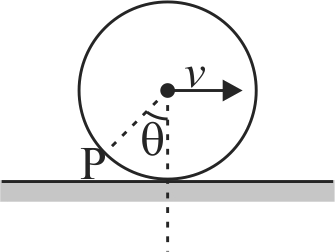
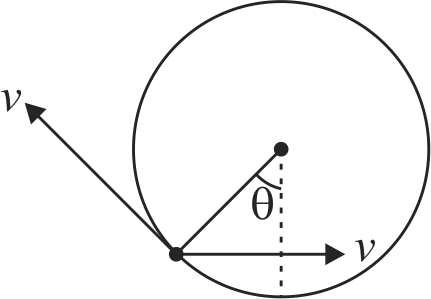
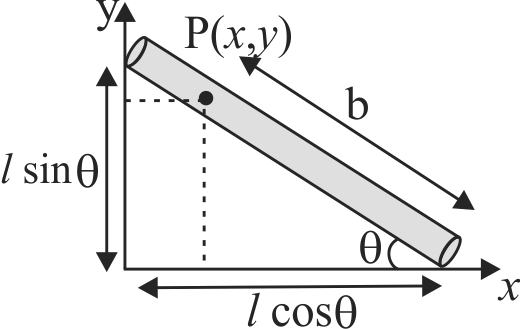
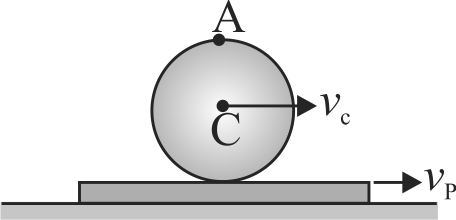
A large spool of rope stands on the ground with the end of the rope lying on the top edge of the spool. A person grabs the end of the rope and walks a distance \(l\), holding onto it. The spool rolls behind the person without slipping. What is the length of rope that unwinds from the spool? How far does the spool's \(CM\) move?
366050
A large spool of rope stands on the ground with the end of the rope lying on the top edge of the spool. A person grabs the end of the rope and walks a distance \(l\), holding onto it. The spool rolls behind the person without slipping. What is the length of rope that unwinds from the spool? How far does the spool's \(CM\) move?
366050
A large spool of rope stands on the ground with the end of the rope lying on the top edge of the spool. A person grabs the end of the rope and walks a distance \(l\), holding onto it. The spool rolls behind the person without slipping. What is the length of rope that unwinds from the spool? How far does the spool's \(CM\) move?
366050
A large spool of rope stands on the ground with the end of the rope lying on the top edge of the spool. A person grabs the end of the rope and walks a distance \(l\), holding onto it. The spool rolls behind the person without slipping. What is the length of rope that unwinds from the spool? How far does the spool's \(CM\) move?