366015
A ring A is initially rolling without sliding with a velocity \(v\) on the horizontal surface of the body B (of same mass as A). All surfaces are smooth. \(B\) has no initial velocity. What will be the maximum height reached by A on \(\mathrm{B}\) ?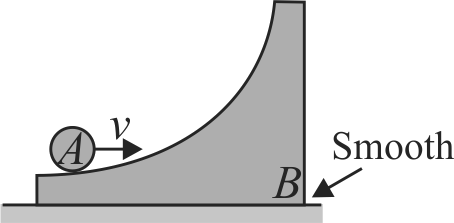
366015
A ring A is initially rolling without sliding with a velocity \(v\) on the horizontal surface of the body B (of same mass as A). All surfaces are smooth. \(B\) has no initial velocity. What will be the maximum height reached by A on \(\mathrm{B}\) ?
366015
A ring A is initially rolling without sliding with a velocity \(v\) on the horizontal surface of the body B (of same mass as A). All surfaces are smooth. \(B\) has no initial velocity. What will be the maximum height reached by A on \(\mathrm{B}\) ?
366015
A ring A is initially rolling without sliding with a velocity \(v\) on the horizontal surface of the body B (of same mass as A). All surfaces are smooth. \(B\) has no initial velocity. What will be the maximum height reached by A on \(\mathrm{B}\) ?
