366003
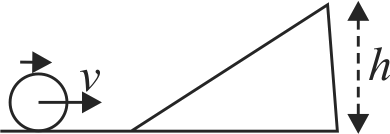
A uniform cylinder (mass 
366003
A uniform cylinder (mass 
366003
A uniform cylinder (mass 
366003
A uniform cylinder (mass 
366003
A uniform cylinder (mass