Explanation:
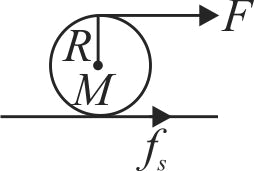
Here, \(f_{s}\) will be in the forward direction for sphere. \(F\) and \(f_{s}\) both will contribute in linear and angular accelerations.
\(\left( {F + {f_s}} \right) = M \times a\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
\(\left( {F - {f_s}} \right)R = I\alpha \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)
For pure acceleration rolling
\(a = R\alpha \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right)\)