365973
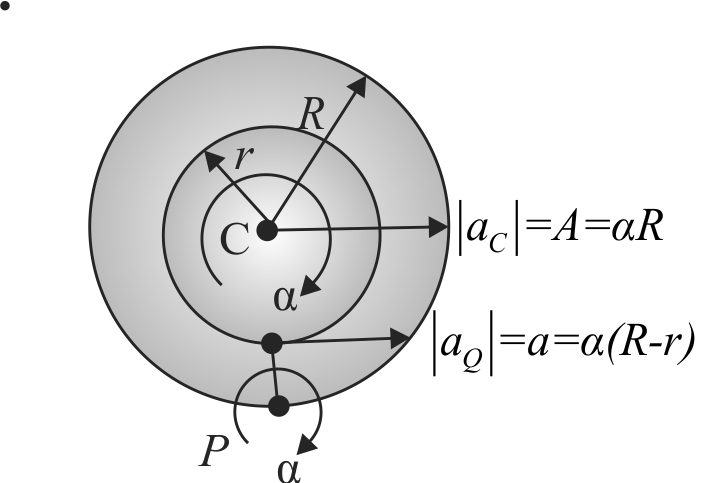
A bobbin has inner radius \(r\) and outer radius \(R\) is placed on a rough horizontal surface. A light is string wrapped over inner core, connects a block with bobbin as shown in the figure. Now system is released from rest and bobbin moves on the horizontal surface without sliding, and the string does not slide from bobbin, If \(\dfrac{r}{R}=0.25\), find the ratio of the acceleration of the block and bobbin \(\left(\dfrac{a}{A}\right)\).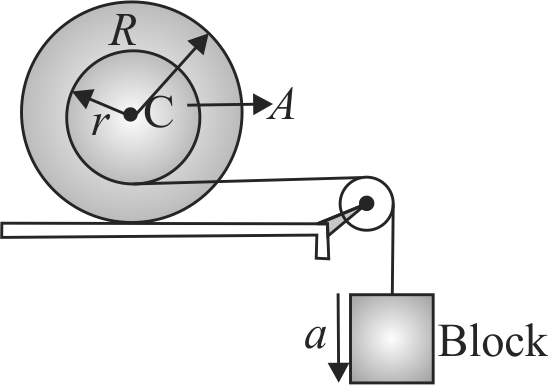
365974
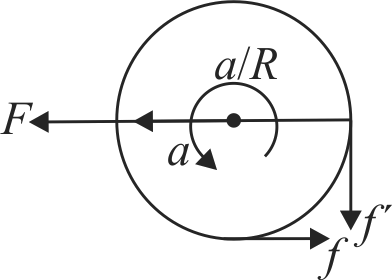
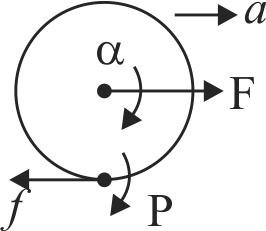
A boy is pushing a ring of mass 2 \(kg\) and radius 0.5 \(m\) with a stick as shown in the figure. The stick applies a force of 2 \(N\) on the ring and rolls it without slipping with an acceleration of \(0.3\;m/{s^2}.\) The coefficient of friction between the ground and the ring is large enough that rolling always occurs and the coefficient of friction between the stick and the ring is \((P / 10)\). Find the value of \(P\)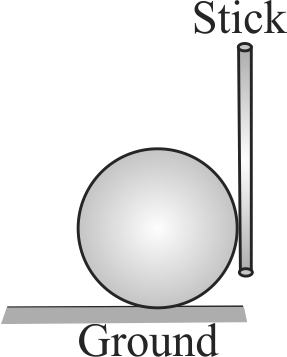
365973
A bobbin has inner radius \(r\) and outer radius \(R\) is placed on a rough horizontal surface. A light is string wrapped over inner core, connects a block with bobbin as shown in the figure. Now system is released from rest and bobbin moves on the horizontal surface without sliding, and the string does not slide from bobbin, If \(\dfrac{r}{R}=0.25\), find the ratio of the acceleration of the block and bobbin \(\left(\dfrac{a}{A}\right)\).
365974
A boy is pushing a ring of mass 2 \(kg\) and radius 0.5 \(m\) with a stick as shown in the figure. The stick applies a force of 2 \(N\) on the ring and rolls it without slipping with an acceleration of \(0.3\;m/{s^2}.\) The coefficient of friction between the ground and the ring is large enough that rolling always occurs and the coefficient of friction between the stick and the ring is \((P / 10)\). Find the value of \(P\)
365973
A bobbin has inner radius \(r\) and outer radius \(R\) is placed on a rough horizontal surface. A light is string wrapped over inner core, connects a block with bobbin as shown in the figure. Now system is released from rest and bobbin moves on the horizontal surface without sliding, and the string does not slide from bobbin, If \(\dfrac{r}{R}=0.25\), find the ratio of the acceleration of the block and bobbin \(\left(\dfrac{a}{A}\right)\).
365974
A boy is pushing a ring of mass 2 \(kg\) and radius 0.5 \(m\) with a stick as shown in the figure. The stick applies a force of 2 \(N\) on the ring and rolls it without slipping with an acceleration of \(0.3\;m/{s^2}.\) The coefficient of friction between the ground and the ring is large enough that rolling always occurs and the coefficient of friction between the stick and the ring is \((P / 10)\). Find the value of \(P\)
365973
A bobbin has inner radius \(r\) and outer radius \(R\) is placed on a rough horizontal surface. A light is string wrapped over inner core, connects a block with bobbin as shown in the figure. Now system is released from rest and bobbin moves on the horizontal surface without sliding, and the string does not slide from bobbin, If \(\dfrac{r}{R}=0.25\), find the ratio of the acceleration of the block and bobbin \(\left(\dfrac{a}{A}\right)\).
365974
A boy is pushing a ring of mass 2 \(kg\) and radius 0.5 \(m\) with a stick as shown in the figure. The stick applies a force of 2 \(N\) on the ring and rolls it without slipping with an acceleration of \(0.3\;m/{s^2}.\) The coefficient of friction between the ground and the ring is large enough that rolling always occurs and the coefficient of friction between the stick and the ring is \((P / 10)\). Find the value of \(P\)
365973
A bobbin has inner radius \(r\) and outer radius \(R\) is placed on a rough horizontal surface. A light is string wrapped over inner core, connects a block with bobbin as shown in the figure. Now system is released from rest and bobbin moves on the horizontal surface without sliding, and the string does not slide from bobbin, If \(\dfrac{r}{R}=0.25\), find the ratio of the acceleration of the block and bobbin \(\left(\dfrac{a}{A}\right)\).
365974
A boy is pushing a ring of mass 2 \(kg\) and radius 0.5 \(m\) with a stick as shown in the figure. The stick applies a force of 2 \(N\) on the ring and rolls it without slipping with an acceleration of \(0.3\;m/{s^2}.\) The coefficient of friction between the ground and the ring is large enough that rolling always occurs and the coefficient of friction between the stick and the ring is \((P / 10)\). Find the value of \(P\)