366041 A small solid ball (mass \({=0.1 {~kg}}\)) rolls without slipping along the track shown in the figure. The radius of the circular track is \({R}\). If the ball starts from rest at a height \({8 R}\) above the bottom, the horizontal force acting on it at point \({P}\) is \({5 x}\) newton. Find the value of \({x}\) (Given, \({g=10 {~ms}^{-2}}\))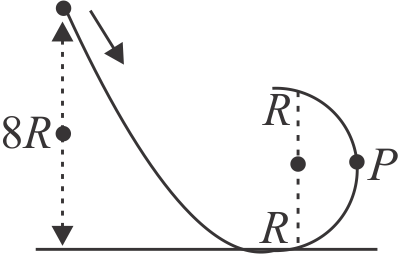

366042 A hoop of radius \(2\;m\) weights \(100\;kg\). It rolls along a horizontal floor so that its centre of mass has a speed of \(20\;cm\;{s^{ - 1}}\). How much work has to be done to stop it?

366043 Assertion :
A body rolls down an inclined plane without slipping. The fraction of total energy associated with its rotation will depend on its radius of gyration.
Reason :
Total kinetic energy of rolling body is equal to addition of kinetic energy of rotation and kinetic energy of translation.

366044 A solid sphere rolls down from top of inclined plane \(7\;m\) high without slipping. Its linear speed at the foot of plane is \(\left( {g = 10\;m/{s^2}} \right)\)

366041 A small solid ball (mass \({=0.1 {~kg}}\)) rolls without slipping along the track shown in the figure. The radius of the circular track is \({R}\). If the ball starts from rest at a height \({8 R}\) above the bottom, the horizontal force acting on it at point \({P}\) is \({5 x}\) newton. Find the value of \({x}\) (Given, \({g=10 {~ms}^{-2}}\))

366042 A hoop of radius \(2\;m\) weights \(100\;kg\). It rolls along a horizontal floor so that its centre of mass has a speed of \(20\;cm\;{s^{ - 1}}\). How much work has to be done to stop it?

366043 Assertion :
A body rolls down an inclined plane without slipping. The fraction of total energy associated with its rotation will depend on its radius of gyration.
Reason :
Total kinetic energy of rolling body is equal to addition of kinetic energy of rotation and kinetic energy of translation.

366044 A solid sphere rolls down from top of inclined plane \(7\;m\) high without slipping. Its linear speed at the foot of plane is \(\left( {g = 10\;m/{s^2}} \right)\)

366041 A small solid ball (mass \({=0.1 {~kg}}\)) rolls without slipping along the track shown in the figure. The radius of the circular track is \({R}\). If the ball starts from rest at a height \({8 R}\) above the bottom, the horizontal force acting on it at point \({P}\) is \({5 x}\) newton. Find the value of \({x}\) (Given, \({g=10 {~ms}^{-2}}\))

366042 A hoop of radius \(2\;m\) weights \(100\;kg\). It rolls along a horizontal floor so that its centre of mass has a speed of \(20\;cm\;{s^{ - 1}}\). How much work has to be done to stop it?

366043 Assertion :
A body rolls down an inclined plane without slipping. The fraction of total energy associated with its rotation will depend on its radius of gyration.
Reason :
Total kinetic energy of rolling body is equal to addition of kinetic energy of rotation and kinetic energy of translation.

366044 A solid sphere rolls down from top of inclined plane \(7\;m\) high without slipping. Its linear speed at the foot of plane is \(\left( {g = 10\;m/{s^2}} \right)\)

366041 A small solid ball (mass \({=0.1 {~kg}}\)) rolls without slipping along the track shown in the figure. The radius of the circular track is \({R}\). If the ball starts from rest at a height \({8 R}\) above the bottom, the horizontal force acting on it at point \({P}\) is \({5 x}\) newton. Find the value of \({x}\) (Given, \({g=10 {~ms}^{-2}}\))

366042 A hoop of radius \(2\;m\) weights \(100\;kg\). It rolls along a horizontal floor so that its centre of mass has a speed of \(20\;cm\;{s^{ - 1}}\). How much work has to be done to stop it?

366043 Assertion :
A body rolls down an inclined plane without slipping. The fraction of total energy associated with its rotation will depend on its radius of gyration.
Reason :
Total kinetic energy of rolling body is equal to addition of kinetic energy of rotation and kinetic energy of translation.

366044 A solid sphere rolls down from top of inclined plane \(7\;m\) high without slipping. Its linear speed at the foot of plane is \(\left( {g = 10\;m/{s^2}} \right)\)