366037 A solid sphere of mass \(m\) rolls down an inclined plane without slipping, starting from rest at the top of an incined plane. The linear speed of the sphere at the bottom of the inclined plane is \(v\). The kinetic energy of the sphere at the bottom is
366040
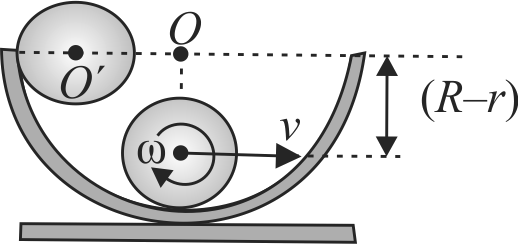
A solid sphere of mass \(m\) and radius \(r\) is released from rest from the given position. The sphere rolls without sliding on the circular track of radius \(R=8 r\). If \(r=1 {~m}\) then find its speed when it reaches its lowest position. (Take \(g=10 {~m} / {s}^{2}\) )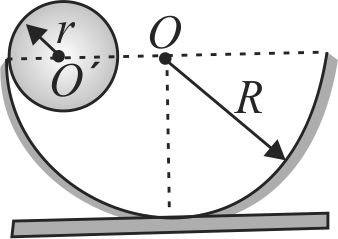
366037 A solid sphere of mass \(m\) rolls down an inclined plane without slipping, starting from rest at the top of an incined plane. The linear speed of the sphere at the bottom of the inclined plane is \(v\). The kinetic energy of the sphere at the bottom is
366040
A solid sphere of mass \(m\) and radius \(r\) is released from rest from the given position. The sphere rolls without sliding on the circular track of radius \(R=8 r\). If \(r=1 {~m}\) then find its speed when it reaches its lowest position. (Take \(g=10 {~m} / {s}^{2}\) )
366037 A solid sphere of mass \(m\) rolls down an inclined plane without slipping, starting from rest at the top of an incined plane. The linear speed of the sphere at the bottom of the inclined plane is \(v\). The kinetic energy of the sphere at the bottom is
366040
A solid sphere of mass \(m\) and radius \(r\) is released from rest from the given position. The sphere rolls without sliding on the circular track of radius \(R=8 r\). If \(r=1 {~m}\) then find its speed when it reaches its lowest position. (Take \(g=10 {~m} / {s}^{2}\) )
366037 A solid sphere of mass \(m\) rolls down an inclined plane without slipping, starting from rest at the top of an incined plane. The linear speed of the sphere at the bottom of the inclined plane is \(v\). The kinetic energy of the sphere at the bottom is
366040
A solid sphere of mass \(m\) and radius \(r\) is released from rest from the given position. The sphere rolls without sliding on the circular track of radius \(R=8 r\). If \(r=1 {~m}\) then find its speed when it reaches its lowest position. (Take \(g=10 {~m} / {s}^{2}\) )