366003
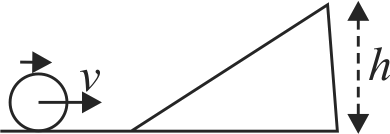
A uniform cylinder (mass \(M\) ) of radius \(R\) is kept on an accelerating platform (mass \(M\) ) as shown in figure. If the cylinder rolls without slipping on the platform, determine the magnitude of acceleration of the centre of mass of cylinder. Assuming the coefficient of friction \(\mu=0.4\). determine the maximum acceleration of the platform may have without slip between the cylinder and the platform. (Take \(g=10 {~m} / {s}^{2}\) )
366006
A cylinder of mass \(M_{c}\) and sphere of mass \(M_{s}\) are placed at points \(\mathrm{A}\) and \(\mathrm{B}\) of two inclines respectively. (See Figure). If they roll on the incline without slipping such that their accelerations are the same, then ratio of \(\dfrac{\sin \theta_{\mathrm{C}}}{\sin \theta_{\mathrm{s}}}\) is :
366003
A uniform cylinder (mass \(M\) ) of radius \(R\) is kept on an accelerating platform (mass \(M\) ) as shown in figure. If the cylinder rolls without slipping on the platform, determine the magnitude of acceleration of the centre of mass of cylinder. Assuming the coefficient of friction \(\mu=0.4\). determine the maximum acceleration of the platform may have without slip between the cylinder and the platform. (Take \(g=10 {~m} / {s}^{2}\) )
366006
A cylinder of mass \(M_{c}\) and sphere of mass \(M_{s}\) are placed at points \(\mathrm{A}\) and \(\mathrm{B}\) of two inclines respectively. (See Figure). If they roll on the incline without slipping such that their accelerations are the same, then ratio of \(\dfrac{\sin \theta_{\mathrm{C}}}{\sin \theta_{\mathrm{s}}}\) is :
366003
A uniform cylinder (mass \(M\) ) of radius \(R\) is kept on an accelerating platform (mass \(M\) ) as shown in figure. If the cylinder rolls without slipping on the platform, determine the magnitude of acceleration of the centre of mass of cylinder. Assuming the coefficient of friction \(\mu=0.4\). determine the maximum acceleration of the platform may have without slip between the cylinder and the platform. (Take \(g=10 {~m} / {s}^{2}\) )
366006
A cylinder of mass \(M_{c}\) and sphere of mass \(M_{s}\) are placed at points \(\mathrm{A}\) and \(\mathrm{B}\) of two inclines respectively. (See Figure). If they roll on the incline without slipping such that their accelerations are the same, then ratio of \(\dfrac{\sin \theta_{\mathrm{C}}}{\sin \theta_{\mathrm{s}}}\) is :
366003
A uniform cylinder (mass \(M\) ) of radius \(R\) is kept on an accelerating platform (mass \(M\) ) as shown in figure. If the cylinder rolls without slipping on the platform, determine the magnitude of acceleration of the centre of mass of cylinder. Assuming the coefficient of friction \(\mu=0.4\). determine the maximum acceleration of the platform may have without slip between the cylinder and the platform. (Take \(g=10 {~m} / {s}^{2}\) )
366006
A cylinder of mass \(M_{c}\) and sphere of mass \(M_{s}\) are placed at points \(\mathrm{A}\) and \(\mathrm{B}\) of two inclines respectively. (See Figure). If they roll on the incline without slipping such that their accelerations are the same, then ratio of \(\dfrac{\sin \theta_{\mathrm{C}}}{\sin \theta_{\mathrm{s}}}\) is :
366003
A uniform cylinder (mass \(M\) ) of radius \(R\) is kept on an accelerating platform (mass \(M\) ) as shown in figure. If the cylinder rolls without slipping on the platform, determine the magnitude of acceleration of the centre of mass of cylinder. Assuming the coefficient of friction \(\mu=0.4\). determine the maximum acceleration of the platform may have without slip between the cylinder and the platform. (Take \(g=10 {~m} / {s}^{2}\) )
366006
A cylinder of mass \(M_{c}\) and sphere of mass \(M_{s}\) are placed at points \(\mathrm{A}\) and \(\mathrm{B}\) of two inclines respectively. (See Figure). If they roll on the incline without slipping such that their accelerations are the same, then ratio of \(\dfrac{\sin \theta_{\mathrm{C}}}{\sin \theta_{\mathrm{s}}}\) is :