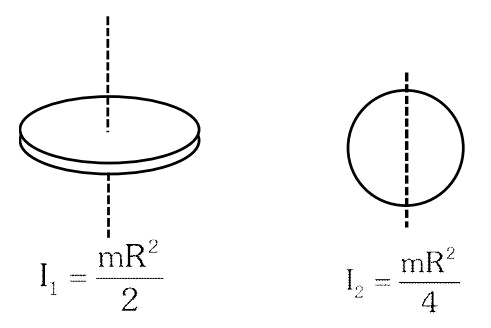
365861 One quarter of the plate is cut from a square plate as shown in the figure. If \(M'\) is the mass of the plate and \(\ell\) is the length of each side, then the moment of inertia of the plate about an axis passing through \(O'\) and perpendicular to the plate is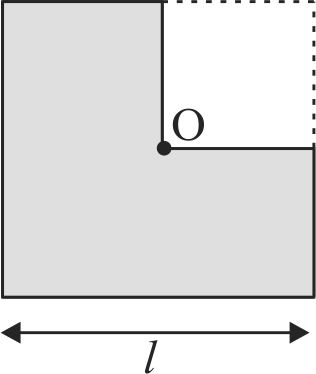

365862 From a circular ring of mass ' \(M\) ' and radius ' \(R\) ' an arc corresponding to a \(90^{\circ}\) sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is \('K'\) times \('M{R^2}\). Then the value of \('K'\) is

365863 The ratio of the radius of gyration of a thin unifrom disc about an axis passing through its centre and normal to its plane to the radius of gyration of the disc about its diameter is

365864 A ring of mass \(m\) and radius \(r\) is melted and then moulded into a sphere. The moment of inertia of the sphere will be

365865 Two discs have same mass and thickness. Their materials have densities \(d_{1}\) and \(d_{2}\). The ratio of their moments of inertia about central axis will be

365861 One quarter of the plate is cut from a square plate as shown in the figure. If \(M'\) is the mass of the plate and \(\ell\) is the length of each side, then the moment of inertia of the plate about an axis passing through \(O'\) and perpendicular to the plate is

365862 From a circular ring of mass ' \(M\) ' and radius ' \(R\) ' an arc corresponding to a \(90^{\circ}\) sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is \('K'\) times \('M{R^2}\). Then the value of \('K'\) is

365863 The ratio of the radius of gyration of a thin unifrom disc about an axis passing through its centre and normal to its plane to the radius of gyration of the disc about its diameter is

365864 A ring of mass \(m\) and radius \(r\) is melted and then moulded into a sphere. The moment of inertia of the sphere will be

365865 Two discs have same mass and thickness. Their materials have densities \(d_{1}\) and \(d_{2}\). The ratio of their moments of inertia about central axis will be

365861 One quarter of the plate is cut from a square plate as shown in the figure. If \(M'\) is the mass of the plate and \(\ell\) is the length of each side, then the moment of inertia of the plate about an axis passing through \(O'\) and perpendicular to the plate is

365862 From a circular ring of mass ' \(M\) ' and radius ' \(R\) ' an arc corresponding to a \(90^{\circ}\) sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is \('K'\) times \('M{R^2}\). Then the value of \('K'\) is

365863 The ratio of the radius of gyration of a thin unifrom disc about an axis passing through its centre and normal to its plane to the radius of gyration of the disc about its diameter is

365864 A ring of mass \(m\) and radius \(r\) is melted and then moulded into a sphere. The moment of inertia of the sphere will be

365865 Two discs have same mass and thickness. Their materials have densities \(d_{1}\) and \(d_{2}\). The ratio of their moments of inertia about central axis will be

365861 One quarter of the plate is cut from a square plate as shown in the figure. If \(M'\) is the mass of the plate and \(\ell\) is the length of each side, then the moment of inertia of the plate about an axis passing through \(O'\) and perpendicular to the plate is

365862 From a circular ring of mass ' \(M\) ' and radius ' \(R\) ' an arc corresponding to a \(90^{\circ}\) sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is \('K'\) times \('M{R^2}\). Then the value of \('K'\) is

365863 The ratio of the radius of gyration of a thin unifrom disc about an axis passing through its centre and normal to its plane to the radius of gyration of the disc about its diameter is

365864 A ring of mass \(m\) and radius \(r\) is melted and then moulded into a sphere. The moment of inertia of the sphere will be

365865 Two discs have same mass and thickness. Their materials have densities \(d_{1}\) and \(d_{2}\). The ratio of their moments of inertia about central axis will be

365861 One quarter of the plate is cut from a square plate as shown in the figure. If \(M'\) is the mass of the plate and \(\ell\) is the length of each side, then the moment of inertia of the plate about an axis passing through \(O'\) and perpendicular to the plate is

365862 From a circular ring of mass ' \(M\) ' and radius ' \(R\) ' an arc corresponding to a \(90^{\circ}\) sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is \('K'\) times \('M{R^2}\). Then the value of \('K'\) is

365863 The ratio of the radius of gyration of a thin unifrom disc about an axis passing through its centre and normal to its plane to the radius of gyration of the disc about its diameter is

365864 A ring of mass \(m\) and radius \(r\) is melted and then moulded into a sphere. The moment of inertia of the sphere will be

365865 Two discs have same mass and thickness. Their materials have densities \(d_{1}\) and \(d_{2}\). The ratio of their moments of inertia about central axis will be