365855
Moment of inertia of an equilateral triangular lamina \(A B C\), about the axis passing through its centre \(\mathrm{O}\) and perpendicular to its plane is \(I_{0}\) as shown in the figure. A cavity DEF is cut out from the lamina, where D, E, F are the mid points of the sides. Moment of inertia of the remaining part of lamina about the same axis is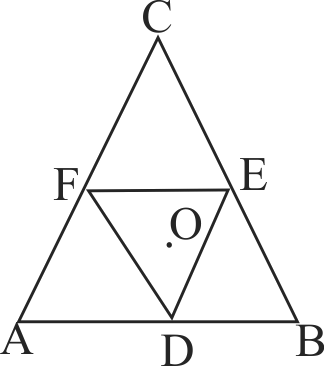
365856
From a uniform circular disc of radius \(R\) and mass \(9M\), a small disc of radius \(\dfrac{R}{3}\) is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :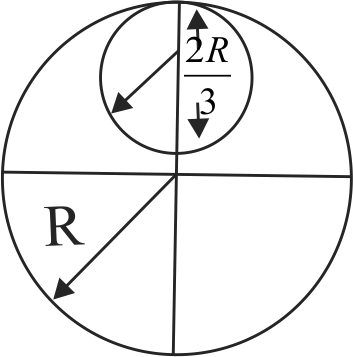
365855
Moment of inertia of an equilateral triangular lamina \(A B C\), about the axis passing through its centre \(\mathrm{O}\) and perpendicular to its plane is \(I_{0}\) as shown in the figure. A cavity DEF is cut out from the lamina, where D, E, F are the mid points of the sides. Moment of inertia of the remaining part of lamina about the same axis is
365856
From a uniform circular disc of radius \(R\) and mass \(9M\), a small disc of radius \(\dfrac{R}{3}\) is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :
365855
Moment of inertia of an equilateral triangular lamina \(A B C\), about the axis passing through its centre \(\mathrm{O}\) and perpendicular to its plane is \(I_{0}\) as shown in the figure. A cavity DEF is cut out from the lamina, where D, E, F are the mid points of the sides. Moment of inertia of the remaining part of lamina about the same axis is
365856
From a uniform circular disc of radius \(R\) and mass \(9M\), a small disc of radius \(\dfrac{R}{3}\) is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :
365855
Moment of inertia of an equilateral triangular lamina \(A B C\), about the axis passing through its centre \(\mathrm{O}\) and perpendicular to its plane is \(I_{0}\) as shown in the figure. A cavity DEF is cut out from the lamina, where D, E, F are the mid points of the sides. Moment of inertia of the remaining part of lamina about the same axis is
365856
From a uniform circular disc of radius \(R\) and mass \(9M\), a small disc of radius \(\dfrac{R}{3}\) is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :
.png)