365815 A bomb of mass ' \(m\) ' at rest at the coordinate origin explodes into three equal pieces. At a certain instant one piece is on the \(x\)-axis at \(x = 40\;cm\) and another is at \(x = 20\;\,cm,{\rm{ }}y = - 60\;\,cm\). The position of the third piece is
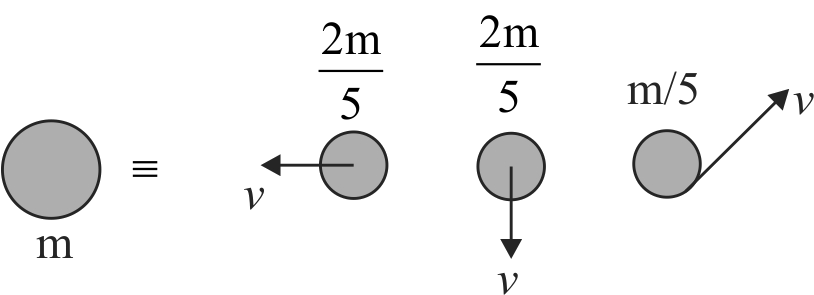
365818 A shell of mass \(m\) which is at rest initially. It explodes into three fragments having masses in the ratio \(2: 2: 1\). If the fragments having equal masses fly off along mutually perpendicualr directions with speed \(v\), the speed of the third (lighter) fragment is
365815 A bomb of mass ' \(m\) ' at rest at the coordinate origin explodes into three equal pieces. At a certain instant one piece is on the \(x\)-axis at \(x = 40\;cm\) and another is at \(x = 20\;\,cm,{\rm{ }}y = - 60\;\,cm\). The position of the third piece is
365818 A shell of mass \(m\) which is at rest initially. It explodes into three fragments having masses in the ratio \(2: 2: 1\). If the fragments having equal masses fly off along mutually perpendicualr directions with speed \(v\), the speed of the third (lighter) fragment is
365815 A bomb of mass ' \(m\) ' at rest at the coordinate origin explodes into three equal pieces. At a certain instant one piece is on the \(x\)-axis at \(x = 40\;cm\) and another is at \(x = 20\;\,cm,{\rm{ }}y = - 60\;\,cm\). The position of the third piece is
365818 A shell of mass \(m\) which is at rest initially. It explodes into three fragments having masses in the ratio \(2: 2: 1\). If the fragments having equal masses fly off along mutually perpendicualr directions with speed \(v\), the speed of the third (lighter) fragment is
365815 A bomb of mass ' \(m\) ' at rest at the coordinate origin explodes into three equal pieces. At a certain instant one piece is on the \(x\)-axis at \(x = 40\;cm\) and another is at \(x = 20\;\,cm,{\rm{ }}y = - 60\;\,cm\). The position of the third piece is
365818 A shell of mass \(m\) which is at rest initially. It explodes into three fragments having masses in the ratio \(2: 2: 1\). If the fragments having equal masses fly off along mutually perpendicualr directions with speed \(v\), the speed of the third (lighter) fragment is
365815 A bomb of mass ' \(m\) ' at rest at the coordinate origin explodes into three equal pieces. At a certain instant one piece is on the \(x\)-axis at \(x = 40\;cm\) and another is at \(x = 20\;\,cm,{\rm{ }}y = - 60\;\,cm\). The position of the third piece is
365818 A shell of mass \(m\) which is at rest initially. It explodes into three fragments having masses in the ratio \(2: 2: 1\). If the fragments having equal masses fly off along mutually perpendicualr directions with speed \(v\), the speed of the third (lighter) fragment is