365767
In a vertical plane inside a smooth hollow thin tube a block of same mass as that of tube is released as shown in the figure. When it is slightly disturbed it moves towards right. By the time the block reaches the right end of the tube, displacement of the tube will be (where ' \(R\) ' is mean radius of tube). Assume that the tube remains in vertical plane.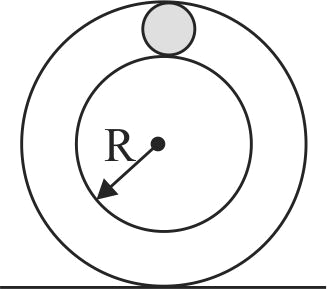
365768 Centre of mass of a particle of mass \(6\;kg\) is at the point \((1 m, 2 m, 3 m)\) and center of mass of another mass \(5\;kg\) is at point \(( - 1\;m,\,\,3\;m,\, - 2\;m)\). Where a \(5\;kg\) particle should be placed, so that center of mass of the system of all three particles shifts to centre of mass of the first particle?
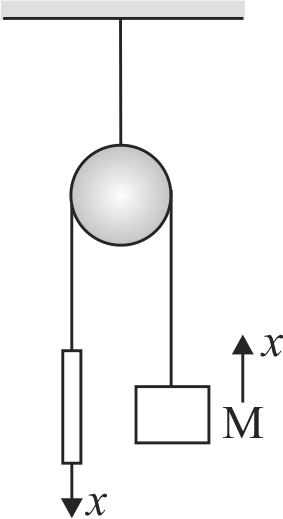
365769 A stationary pulley carries a rope one end of which supports a ladder with a man and the other a counter weight of mass \(M\). The man of mass \(\mathrm{m}\) climbs up a distance \(l\) w.r.to, the ladder and then stops. The displacement of the centre of mass of this system is:
365770
The inclined surfaces of two movable wedges of same mass \(M\) are smoothly conjugated with the horizontal plane as shown in the figure. A washer of mass \(m\) slides down the left wedge from a height \(h\). To what maximum height will the washer rise along the right wedge? Neglect friction.
365767
In a vertical plane inside a smooth hollow thin tube a block of same mass as that of tube is released as shown in the figure. When it is slightly disturbed it moves towards right. By the time the block reaches the right end of the tube, displacement of the tube will be (where ' \(R\) ' is mean radius of tube). Assume that the tube remains in vertical plane.
365768 Centre of mass of a particle of mass \(6\;kg\) is at the point \((1 m, 2 m, 3 m)\) and center of mass of another mass \(5\;kg\) is at point \(( - 1\;m,\,\,3\;m,\, - 2\;m)\). Where a \(5\;kg\) particle should be placed, so that center of mass of the system of all three particles shifts to centre of mass of the first particle?
365769 A stationary pulley carries a rope one end of which supports a ladder with a man and the other a counter weight of mass \(M\). The man of mass \(\mathrm{m}\) climbs up a distance \(l\) w.r.to, the ladder and then stops. The displacement of the centre of mass of this system is:
365770
The inclined surfaces of two movable wedges of same mass \(M\) are smoothly conjugated with the horizontal plane as shown in the figure. A washer of mass \(m\) slides down the left wedge from a height \(h\). To what maximum height will the washer rise along the right wedge? Neglect friction.
365767
In a vertical plane inside a smooth hollow thin tube a block of same mass as that of tube is released as shown in the figure. When it is slightly disturbed it moves towards right. By the time the block reaches the right end of the tube, displacement of the tube will be (where ' \(R\) ' is mean radius of tube). Assume that the tube remains in vertical plane.
365768 Centre of mass of a particle of mass \(6\;kg\) is at the point \((1 m, 2 m, 3 m)\) and center of mass of another mass \(5\;kg\) is at point \(( - 1\;m,\,\,3\;m,\, - 2\;m)\). Where a \(5\;kg\) particle should be placed, so that center of mass of the system of all three particles shifts to centre of mass of the first particle?
365769 A stationary pulley carries a rope one end of which supports a ladder with a man and the other a counter weight of mass \(M\). The man of mass \(\mathrm{m}\) climbs up a distance \(l\) w.r.to, the ladder and then stops. The displacement of the centre of mass of this system is:
365770
The inclined surfaces of two movable wedges of same mass \(M\) are smoothly conjugated with the horizontal plane as shown in the figure. A washer of mass \(m\) slides down the left wedge from a height \(h\). To what maximum height will the washer rise along the right wedge? Neglect friction.
365767
In a vertical plane inside a smooth hollow thin tube a block of same mass as that of tube is released as shown in the figure. When it is slightly disturbed it moves towards right. By the time the block reaches the right end of the tube, displacement of the tube will be (where ' \(R\) ' is mean radius of tube). Assume that the tube remains in vertical plane.
365768 Centre of mass of a particle of mass \(6\;kg\) is at the point \((1 m, 2 m, 3 m)\) and center of mass of another mass \(5\;kg\) is at point \(( - 1\;m,\,\,3\;m,\, - 2\;m)\). Where a \(5\;kg\) particle should be placed, so that center of mass of the system of all three particles shifts to centre of mass of the first particle?
365769 A stationary pulley carries a rope one end of which supports a ladder with a man and the other a counter weight of mass \(M\). The man of mass \(\mathrm{m}\) climbs up a distance \(l\) w.r.to, the ladder and then stops. The displacement of the centre of mass of this system is:
365770
The inclined surfaces of two movable wedges of same mass \(M\) are smoothly conjugated with the horizontal plane as shown in the figure. A washer of mass \(m\) slides down the left wedge from a height \(h\). To what maximum height will the washer rise along the right wedge? Neglect friction.
365767
In a vertical plane inside a smooth hollow thin tube a block of same mass as that of tube is released as shown in the figure. When it is slightly disturbed it moves towards right. By the time the block reaches the right end of the tube, displacement of the tube will be (where ' \(R\) ' is mean radius of tube). Assume that the tube remains in vertical plane.
365768 Centre of mass of a particle of mass \(6\;kg\) is at the point \((1 m, 2 m, 3 m)\) and center of mass of another mass \(5\;kg\) is at point \(( - 1\;m,\,\,3\;m,\, - 2\;m)\). Where a \(5\;kg\) particle should be placed, so that center of mass of the system of all three particles shifts to centre of mass of the first particle?
365769 A stationary pulley carries a rope one end of which supports a ladder with a man and the other a counter weight of mass \(M\). The man of mass \(\mathrm{m}\) climbs up a distance \(l\) w.r.to, the ladder and then stops. The displacement of the centre of mass of this system is:
365770
The inclined surfaces of two movable wedges of same mass \(M\) are smoothly conjugated with the horizontal plane as shown in the figure. A washer of mass \(m\) slides down the left wedge from a height \(h\). To what maximum height will the washer rise along the right wedge? Neglect friction.