365684
A man sits on a freely rotating stool holding two dumbbells, each of mass \(2.0\,kg\). When his arms are extended horizontally [Fig. (a)], the dumbbells are \(1.0\,m\) from the axis of rotation and the man rotates with an angular speed of \(0.50\,rad/s\). The moment of inertia of the man plus stool is \({5.0 {~kg} \cdot {m}^{2}}\) and is assumed to be constant. The man pulls the dumbbells inward horizontally to a position \(0.50\,m\) from the rotation axis [Fig. (b)]. Find the new angular speed of the man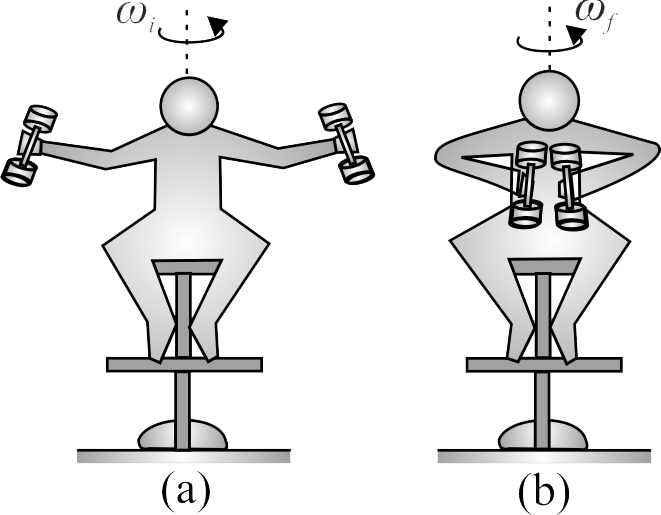
365686
Statement A :
If the total force on the body is zero, then the total linear momentum of the body does not change with time.
Statement B :
If the total torque on the rigid body is zero, the total angular momentum of the body does not change with time.
365687 A thin circular ring of mass \(M\) is rotating about its axis with a constant angular velocity \(\omega\). Two objects, each of mass \(m\), are attached gently to the opposite ends of a diameter of the ring. The ring now rotates with an angular velocity:
365684
A man sits on a freely rotating stool holding two dumbbells, each of mass \(2.0\,kg\). When his arms are extended horizontally [Fig. (a)], the dumbbells are \(1.0\,m\) from the axis of rotation and the man rotates with an angular speed of \(0.50\,rad/s\). The moment of inertia of the man plus stool is \({5.0 {~kg} \cdot {m}^{2}}\) and is assumed to be constant. The man pulls the dumbbells inward horizontally to a position \(0.50\,m\) from the rotation axis [Fig. (b)]. Find the new angular speed of the man
365686
Statement A :
If the total force on the body is zero, then the total linear momentum of the body does not change with time.
Statement B :
If the total torque on the rigid body is zero, the total angular momentum of the body does not change with time.
365687 A thin circular ring of mass \(M\) is rotating about its axis with a constant angular velocity \(\omega\). Two objects, each of mass \(m\), are attached gently to the opposite ends of a diameter of the ring. The ring now rotates with an angular velocity:
365684
A man sits on a freely rotating stool holding two dumbbells, each of mass \(2.0\,kg\). When his arms are extended horizontally [Fig. (a)], the dumbbells are \(1.0\,m\) from the axis of rotation and the man rotates with an angular speed of \(0.50\,rad/s\). The moment of inertia of the man plus stool is \({5.0 {~kg} \cdot {m}^{2}}\) and is assumed to be constant. The man pulls the dumbbells inward horizontally to a position \(0.50\,m\) from the rotation axis [Fig. (b)]. Find the new angular speed of the man
365686
Statement A :
If the total force on the body is zero, then the total linear momentum of the body does not change with time.
Statement B :
If the total torque on the rigid body is zero, the total angular momentum of the body does not change with time.
365687 A thin circular ring of mass \(M\) is rotating about its axis with a constant angular velocity \(\omega\). Two objects, each of mass \(m\), are attached gently to the opposite ends of a diameter of the ring. The ring now rotates with an angular velocity:
365684
A man sits on a freely rotating stool holding two dumbbells, each of mass \(2.0\,kg\). When his arms are extended horizontally [Fig. (a)], the dumbbells are \(1.0\,m\) from the axis of rotation and the man rotates with an angular speed of \(0.50\,rad/s\). The moment of inertia of the man plus stool is \({5.0 {~kg} \cdot {m}^{2}}\) and is assumed to be constant. The man pulls the dumbbells inward horizontally to a position \(0.50\,m\) from the rotation axis [Fig. (b)]. Find the new angular speed of the man
365686
Statement A :
If the total force on the body is zero, then the total linear momentum of the body does not change with time.
Statement B :
If the total torque on the rigid body is zero, the total angular momentum of the body does not change with time.
365687 A thin circular ring of mass \(M\) is rotating about its axis with a constant angular velocity \(\omega\). Two objects, each of mass \(m\), are attached gently to the opposite ends of a diameter of the ring. The ring now rotates with an angular velocity:

