365641
A cockroach of mass ' \({m}\) ' is moving with velocity \({v}\) in anticlockwise sense on the rim of a disc of radius R. The M.I. of the disc about the axis is ' \({I}\) ' and it is rotating in clockwise direction with an angular velocity ' \({\omega}\) '. If the cockroach stops then calculate the angular velocity of disc.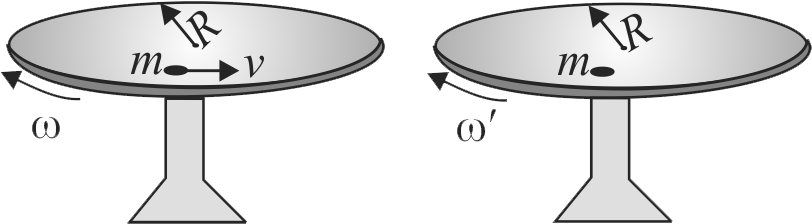
365642
Assertion :
The spin angular velocity of a star is greatly enhanced when it collapse under gravitational pull and become a neutron star.
Reason :
According to law of conservation of angular momentum there is increase in angular velocity of collapsing star.
365644
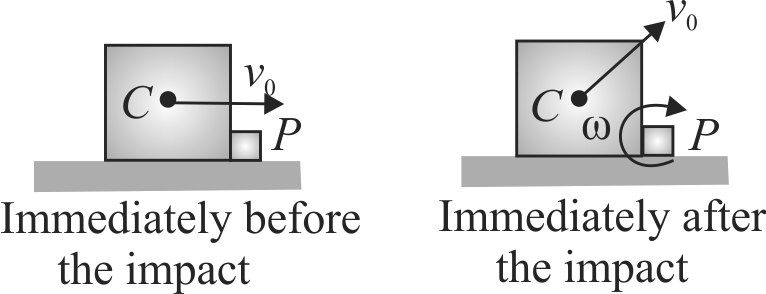
A cube of mass \(m\) and edge length \(l=1 {~m}\) is sliding without friction on a smooth horizontal floor with velocity \(v_{0}=8 {~m} / {s}\) it strikes a long obstruction \(P P\) of small height The obstruction is parallel to the leading bottom edge of the cube. The leading bottom edge of the cube gets pivoted with the obstruction and the cube starts rotating about the edge. Determine angular velocity of the cube immediately after the impact.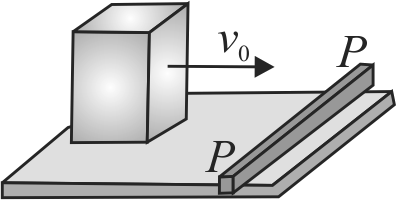
365641
A cockroach of mass ' \({m}\) ' is moving with velocity \({v}\) in anticlockwise sense on the rim of a disc of radius R. The M.I. of the disc about the axis is ' \({I}\) ' and it is rotating in clockwise direction with an angular velocity ' \({\omega}\) '. If the cockroach stops then calculate the angular velocity of disc.
365642
Assertion :
The spin angular velocity of a star is greatly enhanced when it collapse under gravitational pull and become a neutron star.
Reason :
According to law of conservation of angular momentum there is increase in angular velocity of collapsing star.
365644
A cube of mass \(m\) and edge length \(l=1 {~m}\) is sliding without friction on a smooth horizontal floor with velocity \(v_{0}=8 {~m} / {s}\) it strikes a long obstruction \(P P\) of small height The obstruction is parallel to the leading bottom edge of the cube. The leading bottom edge of the cube gets pivoted with the obstruction and the cube starts rotating about the edge. Determine angular velocity of the cube immediately after the impact.
365641
A cockroach of mass ' \({m}\) ' is moving with velocity \({v}\) in anticlockwise sense on the rim of a disc of radius R. The M.I. of the disc about the axis is ' \({I}\) ' and it is rotating in clockwise direction with an angular velocity ' \({\omega}\) '. If the cockroach stops then calculate the angular velocity of disc.
365642
Assertion :
The spin angular velocity of a star is greatly enhanced when it collapse under gravitational pull and become a neutron star.
Reason :
According to law of conservation of angular momentum there is increase in angular velocity of collapsing star.
365644
A cube of mass \(m\) and edge length \(l=1 {~m}\) is sliding without friction on a smooth horizontal floor with velocity \(v_{0}=8 {~m} / {s}\) it strikes a long obstruction \(P P\) of small height The obstruction is parallel to the leading bottom edge of the cube. The leading bottom edge of the cube gets pivoted with the obstruction and the cube starts rotating about the edge. Determine angular velocity of the cube immediately after the impact.
365641
A cockroach of mass ' \({m}\) ' is moving with velocity \({v}\) in anticlockwise sense on the rim of a disc of radius R. The M.I. of the disc about the axis is ' \({I}\) ' and it is rotating in clockwise direction with an angular velocity ' \({\omega}\) '. If the cockroach stops then calculate the angular velocity of disc.
365642
Assertion :
The spin angular velocity of a star is greatly enhanced when it collapse under gravitational pull and become a neutron star.
Reason :
According to law of conservation of angular momentum there is increase in angular velocity of collapsing star.
365644
A cube of mass \(m\) and edge length \(l=1 {~m}\) is sliding without friction on a smooth horizontal floor with velocity \(v_{0}=8 {~m} / {s}\) it strikes a long obstruction \(P P\) of small height The obstruction is parallel to the leading bottom edge of the cube. The leading bottom edge of the cube gets pivoted with the obstruction and the cube starts rotating about the edge. Determine angular velocity of the cube immediately after the impact.
365641
A cockroach of mass ' \({m}\) ' is moving with velocity \({v}\) in anticlockwise sense on the rim of a disc of radius R. The M.I. of the disc about the axis is ' \({I}\) ' and it is rotating in clockwise direction with an angular velocity ' \({\omega}\) '. If the cockroach stops then calculate the angular velocity of disc.
365642
Assertion :
The spin angular velocity of a star is greatly enhanced when it collapse under gravitational pull and become a neutron star.
Reason :
According to law of conservation of angular momentum there is increase in angular velocity of collapsing star.
365644
A cube of mass \(m\) and edge length \(l=1 {~m}\) is sliding without friction on a smooth horizontal floor with velocity \(v_{0}=8 {~m} / {s}\) it strikes a long obstruction \(P P\) of small height The obstruction is parallel to the leading bottom edge of the cube. The leading bottom edge of the cube gets pivoted with the obstruction and the cube starts rotating about the edge. Determine angular velocity of the cube immediately after the impact.