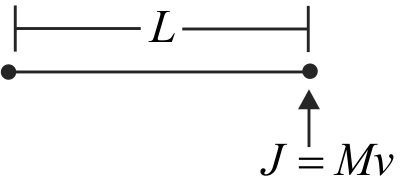
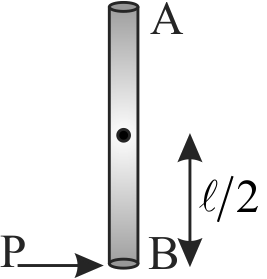
365617 A uniform rod \(A B\) of mass \(m\) and length \(l\) at rest on a smooth horizontal surface. An impulse \(P\) is applied to the end \(B\) in a direction which is perpendicular to the length. The time taken by rod to turn through a right angle is :
365619
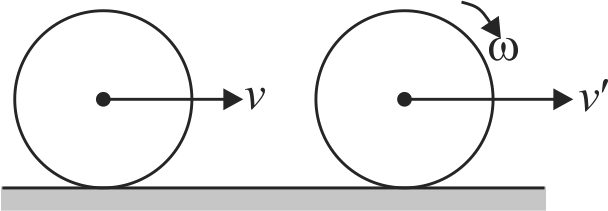
The two uniform discs rotate separately on parallel axles. The upper disc (radius \(a\) and momentum of inertia \(I_{1}\) ) is given an angular velocity \(\omega_{0}\) and the lower disc of (radius \(b\) and momentum of inertia \(I_{2}\) ) is at rest. Now the two discs are moved together so that their rims touch. Final angular velocity of the upper disc is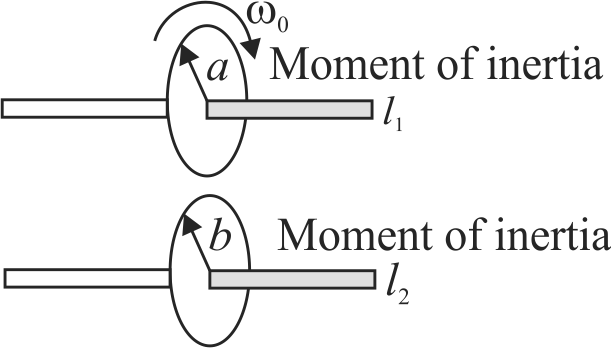
365617 A uniform rod \(A B\) of mass \(m\) and length \(l\) at rest on a smooth horizontal surface. An impulse \(P\) is applied to the end \(B\) in a direction which is perpendicular to the length. The time taken by rod to turn through a right angle is :
365619
The two uniform discs rotate separately on parallel axles. The upper disc (radius \(a\) and momentum of inertia \(I_{1}\) ) is given an angular velocity \(\omega_{0}\) and the lower disc of (radius \(b\) and momentum of inertia \(I_{2}\) ) is at rest. Now the two discs are moved together so that their rims touch. Final angular velocity of the upper disc is
365617 A uniform rod \(A B\) of mass \(m\) and length \(l\) at rest on a smooth horizontal surface. An impulse \(P\) is applied to the end \(B\) in a direction which is perpendicular to the length. The time taken by rod to turn through a right angle is :
365619
The two uniform discs rotate separately on parallel axles. The upper disc (radius \(a\) and momentum of inertia \(I_{1}\) ) is given an angular velocity \(\omega_{0}\) and the lower disc of (radius \(b\) and momentum of inertia \(I_{2}\) ) is at rest. Now the two discs are moved together so that their rims touch. Final angular velocity of the upper disc is
365617 A uniform rod \(A B\) of mass \(m\) and length \(l\) at rest on a smooth horizontal surface. An impulse \(P\) is applied to the end \(B\) in a direction which is perpendicular to the length. The time taken by rod to turn through a right angle is :
365619
The two uniform discs rotate separately on parallel axles. The upper disc (radius \(a\) and momentum of inertia \(I_{1}\) ) is given an angular velocity \(\omega_{0}\) and the lower disc of (radius \(b\) and momentum of inertia \(I_{2}\) ) is at rest. Now the two discs are moved together so that their rims touch. Final angular velocity of the upper disc is
365617 A uniform rod \(A B\) of mass \(m\) and length \(l\) at rest on a smooth horizontal surface. An impulse \(P\) is applied to the end \(B\) in a direction which is perpendicular to the length. The time taken by rod to turn through a right angle is :
365619
The two uniform discs rotate separately on parallel axles. The upper disc (radius \(a\) and momentum of inertia \(I_{1}\) ) is given an angular velocity \(\omega_{0}\) and the lower disc of (radius \(b\) and momentum of inertia \(I_{2}\) ) is at rest. Now the two discs are moved together so that their rims touch. Final angular velocity of the upper disc is