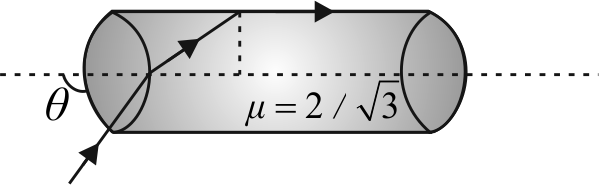
364974 The speed of light in media \({M_1}\) and \({M_2}\) are \(1.5 \times {10^8}m{s^{ - 1}}\)and \(2 \times {10^8}m{s^{ - 1}}\) respectively. A ray travels from medium \({M_1}\) to the medium \({M_2}\) with an angle of incidence \(\theta \) . The ray suffers total internal reflection. Then the value of the angle of incidence \(\theta \) is
364974 The speed of light in media \({M_1}\) and \({M_2}\) are \(1.5 \times {10^8}m{s^{ - 1}}\)and \(2 \times {10^8}m{s^{ - 1}}\) respectively. A ray travels from medium \({M_1}\) to the medium \({M_2}\) with an angle of incidence \(\theta \) . The ray suffers total internal reflection. Then the value of the angle of incidence \(\theta \) is
364974 The speed of light in media \({M_1}\) and \({M_2}\) are \(1.5 \times {10^8}m{s^{ - 1}}\)and \(2 \times {10^8}m{s^{ - 1}}\) respectively. A ray travels from medium \({M_1}\) to the medium \({M_2}\) with an angle of incidence \(\theta \) . The ray suffers total internal reflection. Then the value of the angle of incidence \(\theta \) is
364974 The speed of light in media \({M_1}\) and \({M_2}\) are \(1.5 \times {10^8}m{s^{ - 1}}\)and \(2 \times {10^8}m{s^{ - 1}}\) respectively. A ray travels from medium \({M_1}\) to the medium \({M_2}\) with an angle of incidence \(\theta \) . The ray suffers total internal reflection. Then the value of the angle of incidence \(\theta \) is