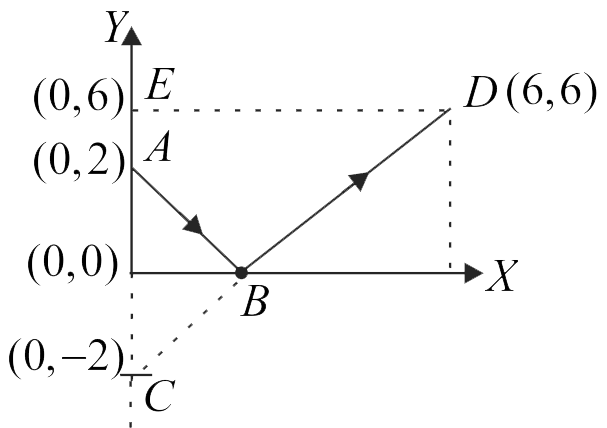
364687 A point source is placed at co-ordinates \((0,2)\) in \({X}-{Y}\) plane. A ray of light from the source is reflected from the \({X}\)-axis. The reflected ray passes through the point \((6,6)\). What is the path length of the ray from \((0,2)\) to \((6,6)\) ?
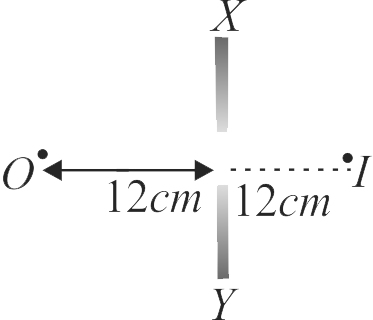
364688 An object is placed at a distance of \(12\;cm\) in front of a plane mirror. The virtual and erect image is formed by the mirror. Now the mirror is moved by \(4\;cm\) towards the stationary object. The distance by which the position of image would be shifted, will be
364687 A point source is placed at co-ordinates \((0,2)\) in \({X}-{Y}\) plane. A ray of light from the source is reflected from the \({X}\)-axis. The reflected ray passes through the point \((6,6)\). What is the path length of the ray from \((0,2)\) to \((6,6)\) ?
364688 An object is placed at a distance of \(12\;cm\) in front of a plane mirror. The virtual and erect image is formed by the mirror. Now the mirror is moved by \(4\;cm\) towards the stationary object. The distance by which the position of image would be shifted, will be
364687 A point source is placed at co-ordinates \((0,2)\) in \({X}-{Y}\) plane. A ray of light from the source is reflected from the \({X}\)-axis. The reflected ray passes through the point \((6,6)\). What is the path length of the ray from \((0,2)\) to \((6,6)\) ?
364688 An object is placed at a distance of \(12\;cm\) in front of a plane mirror. The virtual and erect image is formed by the mirror. Now the mirror is moved by \(4\;cm\) towards the stationary object. The distance by which the position of image would be shifted, will be
364687 A point source is placed at co-ordinates \((0,2)\) in \({X}-{Y}\) plane. A ray of light from the source is reflected from the \({X}\)-axis. The reflected ray passes through the point \((6,6)\). What is the path length of the ray from \((0,2)\) to \((6,6)\) ?
364688 An object is placed at a distance of \(12\;cm\) in front of a plane mirror. The virtual and erect image is formed by the mirror. Now the mirror is moved by \(4\;cm\) towards the stationary object. The distance by which the position of image would be shifted, will be