364520 Consider two SHMs along the same straight line \(x_{1}=A_{1} \sin \left(\omega t+\phi_{1}\right), x_{2}=A_{2} \sin \left(\omega t+\phi_{2}\right)\), where \(A_{1}\) and \(A_{2}\) are their amplitudes and \(\phi_{1}\) and \(\phi_{2}\) are their initial phase angle. If the two SHMs meet simultaneously and ' \(R\) ' is the resultant amplitude, match column I with column II.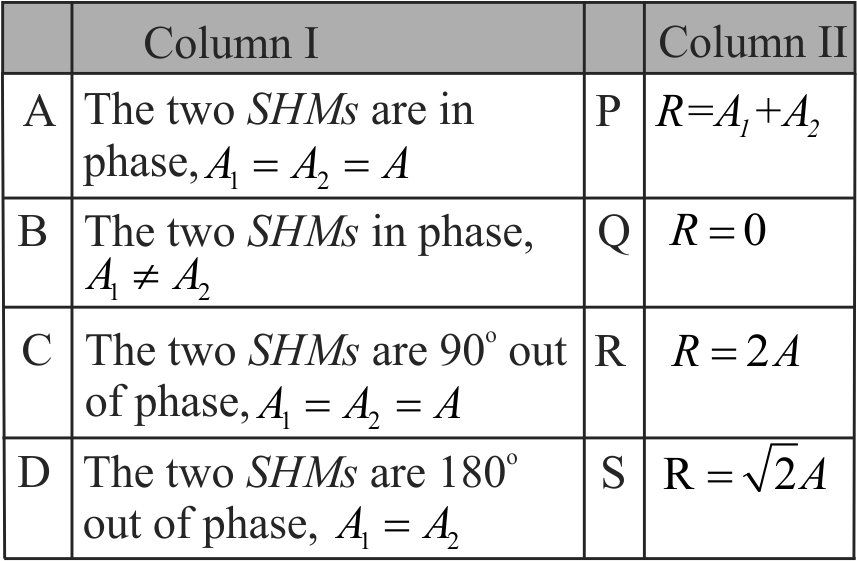

364521 For a periodic motion represented by the equation \(y=\sin \omega t+\cos \omega t\), the amplitude of the motion is

364522 The composition of two simple harmonic motions of equal periods at right angle to each others and with a phase difference of \(\pi\) results in the displacement of the particle along.

364523 The resultant amplitude due to superposition of three simple harmonic motions \({y_1} = 3\sin \omega t{\mkern 1mu} {\mkern 1mu} {y_2} = 5\sin \omega t + {37^{\rm{o}}}\) and \({y_3} = - 15\cos \omega t\) is ____.

364520 Consider two SHMs along the same straight line \(x_{1}=A_{1} \sin \left(\omega t+\phi_{1}\right), x_{2}=A_{2} \sin \left(\omega t+\phi_{2}\right)\), where \(A_{1}\) and \(A_{2}\) are their amplitudes and \(\phi_{1}\) and \(\phi_{2}\) are their initial phase angle. If the two SHMs meet simultaneously and ' \(R\) ' is the resultant amplitude, match column I with column II.

364521 For a periodic motion represented by the equation \(y=\sin \omega t+\cos \omega t\), the amplitude of the motion is

364522 The composition of two simple harmonic motions of equal periods at right angle to each others and with a phase difference of \(\pi\) results in the displacement of the particle along.

364523 The resultant amplitude due to superposition of three simple harmonic motions \({y_1} = 3\sin \omega t{\mkern 1mu} {\mkern 1mu} {y_2} = 5\sin \omega t + {37^{\rm{o}}}\) and \({y_3} = - 15\cos \omega t\) is ____.

364520 Consider two SHMs along the same straight line \(x_{1}=A_{1} \sin \left(\omega t+\phi_{1}\right), x_{2}=A_{2} \sin \left(\omega t+\phi_{2}\right)\), where \(A_{1}\) and \(A_{2}\) are their amplitudes and \(\phi_{1}\) and \(\phi_{2}\) are their initial phase angle. If the two SHMs meet simultaneously and ' \(R\) ' is the resultant amplitude, match column I with column II.

364521 For a periodic motion represented by the equation \(y=\sin \omega t+\cos \omega t\), the amplitude of the motion is

364522 The composition of two simple harmonic motions of equal periods at right angle to each others and with a phase difference of \(\pi\) results in the displacement of the particle along.

364523 The resultant amplitude due to superposition of three simple harmonic motions \({y_1} = 3\sin \omega t{\mkern 1mu} {\mkern 1mu} {y_2} = 5\sin \omega t + {37^{\rm{o}}}\) and \({y_3} = - 15\cos \omega t\) is ____.

364520 Consider two SHMs along the same straight line \(x_{1}=A_{1} \sin \left(\omega t+\phi_{1}\right), x_{2}=A_{2} \sin \left(\omega t+\phi_{2}\right)\), where \(A_{1}\) and \(A_{2}\) are their amplitudes and \(\phi_{1}\) and \(\phi_{2}\) are their initial phase angle. If the two SHMs meet simultaneously and ' \(R\) ' is the resultant amplitude, match column I with column II.

364521 For a periodic motion represented by the equation \(y=\sin \omega t+\cos \omega t\), the amplitude of the motion is

364522 The composition of two simple harmonic motions of equal periods at right angle to each others and with a phase difference of \(\pi\) results in the displacement of the particle along.

364523 The resultant amplitude due to superposition of three simple harmonic motions \({y_1} = 3\sin \omega t{\mkern 1mu} {\mkern 1mu} {y_2} = 5\sin \omega t + {37^{\rm{o}}}\) and \({y_3} = - 15\cos \omega t\) is ____.