364391
Figure shows a block \(P\) of mass \(m\) resting on a horizontal smooth floor at a distance \(l\) from a rigid wall. Block is pushed toward right by a distance \(3{\rm{ }}l/d\) and released, when block passes from its mean position another block of mass \(m_{1}\) is placed on it which sticks to it due to friction. Find the ratio of \(\dfrac{m_{1}}{m}\) so that the combined block just collides with the left wall.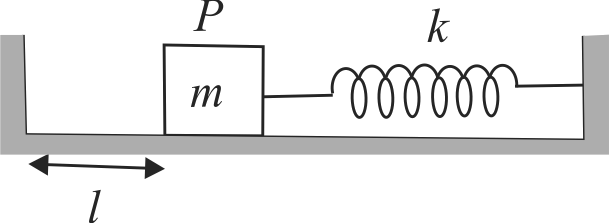
364393
A block \(P\) of mass \(m\) is placed on a smooth horizontal surface. A block \(Q\) of same mass is placed over the block \(P\) and the coefficient of static friction between them is \(\mu_{s}\). A spring of spring constant \(K\) is attached to block \(Q\). The blocks are displaced together to a distance A and released. The upper block oscillates without slipping over the lower block. The maximum frictional force between the block is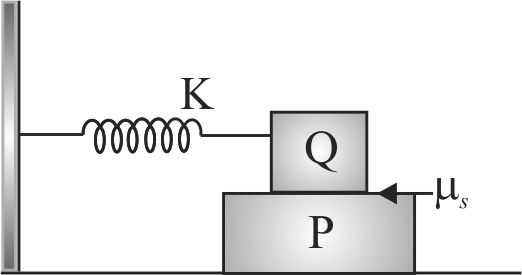
364391
Figure shows a block \(P\) of mass \(m\) resting on a horizontal smooth floor at a distance \(l\) from a rigid wall. Block is pushed toward right by a distance \(3{\rm{ }}l/d\) and released, when block passes from its mean position another block of mass \(m_{1}\) is placed on it which sticks to it due to friction. Find the ratio of \(\dfrac{m_{1}}{m}\) so that the combined block just collides with the left wall.
364393
A block \(P\) of mass \(m\) is placed on a smooth horizontal surface. A block \(Q\) of same mass is placed over the block \(P\) and the coefficient of static friction between them is \(\mu_{s}\). A spring of spring constant \(K\) is attached to block \(Q\). The blocks are displaced together to a distance A and released. The upper block oscillates without slipping over the lower block. The maximum frictional force between the block is
364391
Figure shows a block \(P\) of mass \(m\) resting on a horizontal smooth floor at a distance \(l\) from a rigid wall. Block is pushed toward right by a distance \(3{\rm{ }}l/d\) and released, when block passes from its mean position another block of mass \(m_{1}\) is placed on it which sticks to it due to friction. Find the ratio of \(\dfrac{m_{1}}{m}\) so that the combined block just collides with the left wall.
364393
A block \(P\) of mass \(m\) is placed on a smooth horizontal surface. A block \(Q\) of same mass is placed over the block \(P\) and the coefficient of static friction between them is \(\mu_{s}\). A spring of spring constant \(K\) is attached to block \(Q\). The blocks are displaced together to a distance A and released. The upper block oscillates without slipping over the lower block. The maximum frictional force between the block is
364391
Figure shows a block \(P\) of mass \(m\) resting on a horizontal smooth floor at a distance \(l\) from a rigid wall. Block is pushed toward right by a distance \(3{\rm{ }}l/d\) and released, when block passes from its mean position another block of mass \(m_{1}\) is placed on it which sticks to it due to friction. Find the ratio of \(\dfrac{m_{1}}{m}\) so that the combined block just collides with the left wall.
364393
A block \(P\) of mass \(m\) is placed on a smooth horizontal surface. A block \(Q\) of same mass is placed over the block \(P\) and the coefficient of static friction between them is \(\mu_{s}\). A spring of spring constant \(K\) is attached to block \(Q\). The blocks are displaced together to a distance A and released. The upper block oscillates without slipping over the lower block. The maximum frictional force between the block is
