364384
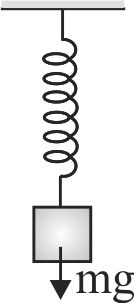
A sphere of mass \({M}\) and radius \({R}\) is on a smooth fixed inclined plane in equilibrium as shown in the figure. If now the sphere is displaced through a small distance along the plane, what will be the angular frequency of the resulting \(SHM\) ?
(Given, \({k=\dfrac{4 M}{3}}\))
364384
A sphere of mass \({M}\) and radius \({R}\) is on a smooth fixed inclined plane in equilibrium as shown in the figure. If now the sphere is displaced through a small distance along the plane, what will be the angular frequency of the resulting \(SHM\) ?
(Given, \({k=\dfrac{4 M}{3}}\))
364384
A sphere of mass \({M}\) and radius \({R}\) is on a smooth fixed inclined plane in equilibrium as shown in the figure. If now the sphere is displaced through a small distance along the plane, what will be the angular frequency of the resulting \(SHM\) ?
(Given, \({k=\dfrac{4 M}{3}}\))
364384
A sphere of mass \({M}\) and radius \({R}\) is on a smooth fixed inclined plane in equilibrium as shown in the figure. If now the sphere is displaced through a small distance along the plane, what will be the angular frequency of the resulting \(SHM\) ?
(Given, \({k=\dfrac{4 M}{3}}\))