1 \(\pi \sqrt{\dfrac{m}{4 K}}\)
2 \(2 \pi \sqrt{\dfrac{m}{K}}\)
3 \(4 \pi \sqrt{\dfrac{m}{K}}\)
4 \(\pi \sqrt{\dfrac{m}{K}}\)
Explanation:
Let us assume that in equilibrium condition spring is \(x_{0}\) elongate from its natural length
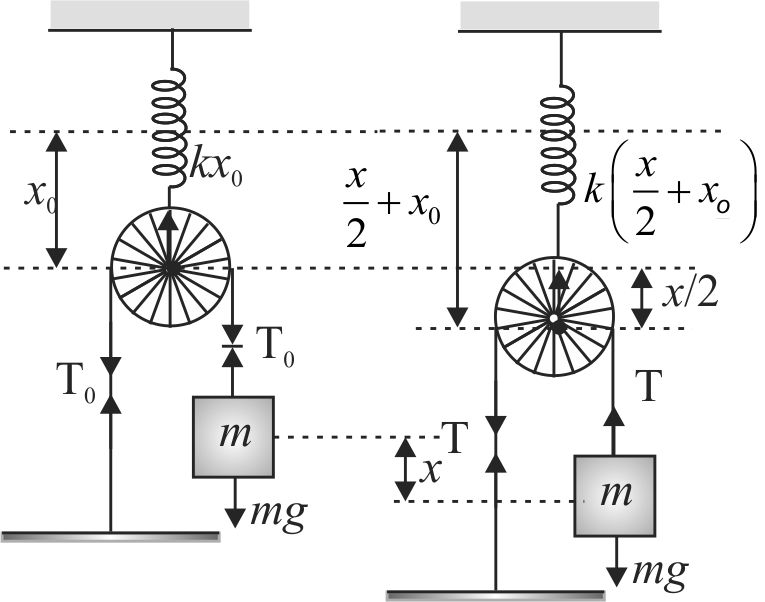
In equilibrium \(T_{0}=m g\)
and \(k x_{0}=2 T_{0}\)
\( \Rightarrow k{x_0} = 2mg\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\)
If the mass \(m\) moves down a distance \(\mathrm{x}\) from its equilibrium position then pulley will move down by \(\dfrac{x}{2}\). So the extra force in spring will be \(\dfrac{k x}{2}\).
From figure
\(\begin{aligned}& F_{\text {net }}=m g-T=m g-\dfrac{k}{2}\left(x_{0}+\dfrac{x}{2}\right) \\& \left(T=\dfrac{k\left(x_{o}+\dfrac{x}{2}\right)}{2}\right) \\& F_{\text {net }}=m g-\dfrac{k x_{0}}{2}-\dfrac{k x}{4}\end{aligned}\)
from eq. (1), we get
\({F_{{\rm{net }}}} = \frac{{ - kx}}{4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2)\)
Comparing eq. (2) with \(F=-K_{\text {Sнм }} x\)
then \(\quad K_{\text {SHM }}=\dfrac{K}{4}\)
\(\Rightarrow T=2 \pi \sqrt{\dfrac{m}{K_{\mathrm{SHM}}}}=2 \pi \sqrt{\dfrac{4 m}{K}}\)