364216 Time period \((T)\) and amplitude (1) are same for two particles which undergo SHM along the same line. At one particular instant, one particle is at phase \(\dfrac{3 \pi}{2}\) and other is at phase zero. While moving in the same direction. Find the time at which they will cross each other.
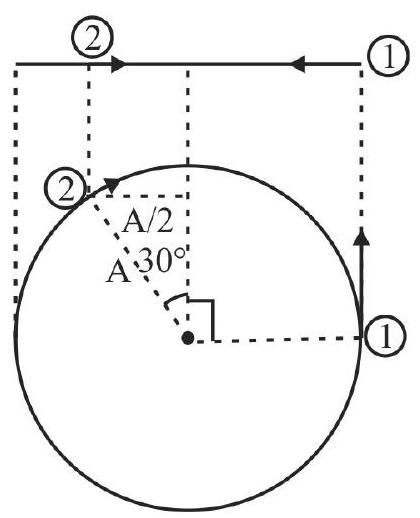
364218 Two particles are performing simple harmonic motion in a straight line about the same equilibrium point. The amplitude and time period for both particles are same and equal to \(A\) and \(T\), respectively. At time \(t = 0\) one particle has displacement A while the other one has displacement \(\frac{{ - A}}{2}\) and they are moving towards each other. If they cross each at time \(t\), then \(t\) is :
364216 Time period \((T)\) and amplitude (1) are same for two particles which undergo SHM along the same line. At one particular instant, one particle is at phase \(\dfrac{3 \pi}{2}\) and other is at phase zero. While moving in the same direction. Find the time at which they will cross each other.
364218 Two particles are performing simple harmonic motion in a straight line about the same equilibrium point. The amplitude and time period for both particles are same and equal to \(A\) and \(T\), respectively. At time \(t = 0\) one particle has displacement A while the other one has displacement \(\frac{{ - A}}{2}\) and they are moving towards each other. If they cross each at time \(t\), then \(t\) is :
364216 Time period \((T)\) and amplitude (1) are same for two particles which undergo SHM along the same line. At one particular instant, one particle is at phase \(\dfrac{3 \pi}{2}\) and other is at phase zero. While moving in the same direction. Find the time at which they will cross each other.
364218 Two particles are performing simple harmonic motion in a straight line about the same equilibrium point. The amplitude and time period for both particles are same and equal to \(A\) and \(T\), respectively. At time \(t = 0\) one particle has displacement A while the other one has displacement \(\frac{{ - A}}{2}\) and they are moving towards each other. If they cross each at time \(t\), then \(t\) is :
364216 Time period \((T)\) and amplitude (1) are same for two particles which undergo SHM along the same line. At one particular instant, one particle is at phase \(\dfrac{3 \pi}{2}\) and other is at phase zero. While moving in the same direction. Find the time at which they will cross each other.
364218 Two particles are performing simple harmonic motion in a straight line about the same equilibrium point. The amplitude and time period for both particles are same and equal to \(A\) and \(T\), respectively. At time \(t = 0\) one particle has displacement A while the other one has displacement \(\frac{{ - A}}{2}\) and they are moving towards each other. If they cross each at time \(t\), then \(t\) is :