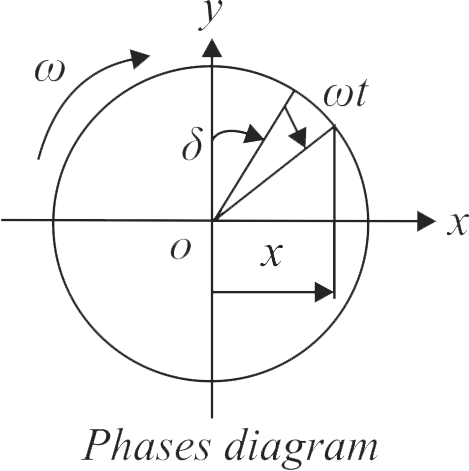
364202 A particle executes \(S.H.M.\) of amplitude \(A\) along \(x\)-axis. At \(t=0\), the position of the particle is \(x=\dfrac{A}{2}\) and it moves along positive \(x\)-axis. The displacement of particle in time \(t\) is \(x=A \sin (\omega t+\delta)\), then the value \(\delta\) will be

364203 A simple harmonic motion having an amplitude \(A\) and time period \(T\) is represented by the equation :
\(y=5 \sin 2 \pi(t+4 x) m\)
Then, the values of \(A\) (in \(m\) ) and \(T\) (in sec) are :

364204 \(x=a \cos ^{2} \omega t\) or \(x=\dfrac{a}{2}-\dfrac{a}{2} \cos 2 \omega t\) represents
(i) Periodic motion but not simple harmonic motion if \(x\) is displacement
(ii) SHM of angular frequency \(2 \omega\)

364205 Which one of the following equations of motion represents simple harmonic motion?

364202 A particle executes \(S.H.M.\) of amplitude \(A\) along \(x\)-axis. At \(t=0\), the position of the particle is \(x=\dfrac{A}{2}\) and it moves along positive \(x\)-axis. The displacement of particle in time \(t\) is \(x=A \sin (\omega t+\delta)\), then the value \(\delta\) will be

364203 A simple harmonic motion having an amplitude \(A\) and time period \(T\) is represented by the equation :
\(y=5 \sin 2 \pi(t+4 x) m\)
Then, the values of \(A\) (in \(m\) ) and \(T\) (in sec) are :

364204 \(x=a \cos ^{2} \omega t\) or \(x=\dfrac{a}{2}-\dfrac{a}{2} \cos 2 \omega t\) represents
(i) Periodic motion but not simple harmonic motion if \(x\) is displacement
(ii) SHM of angular frequency \(2 \omega\)

364205 Which one of the following equations of motion represents simple harmonic motion?

364202 A particle executes \(S.H.M.\) of amplitude \(A\) along \(x\)-axis. At \(t=0\), the position of the particle is \(x=\dfrac{A}{2}\) and it moves along positive \(x\)-axis. The displacement of particle in time \(t\) is \(x=A \sin (\omega t+\delta)\), then the value \(\delta\) will be

364203 A simple harmonic motion having an amplitude \(A\) and time period \(T\) is represented by the equation :
\(y=5 \sin 2 \pi(t+4 x) m\)
Then, the values of \(A\) (in \(m\) ) and \(T\) (in sec) are :

364204 \(x=a \cos ^{2} \omega t\) or \(x=\dfrac{a}{2}-\dfrac{a}{2} \cos 2 \omega t\) represents
(i) Periodic motion but not simple harmonic motion if \(x\) is displacement
(ii) SHM of angular frequency \(2 \omega\)

364205 Which one of the following equations of motion represents simple harmonic motion?

364202 A particle executes \(S.H.M.\) of amplitude \(A\) along \(x\)-axis. At \(t=0\), the position of the particle is \(x=\dfrac{A}{2}\) and it moves along positive \(x\)-axis. The displacement of particle in time \(t\) is \(x=A \sin (\omega t+\delta)\), then the value \(\delta\) will be

364203 A simple harmonic motion having an amplitude \(A\) and time period \(T\) is represented by the equation :
\(y=5 \sin 2 \pi(t+4 x) m\)
Then, the values of \(A\) (in \(m\) ) and \(T\) (in sec) are :

364204 \(x=a \cos ^{2} \omega t\) or \(x=\dfrac{a}{2}-\dfrac{a}{2} \cos 2 \omega t\) represents
(i) Periodic motion but not simple harmonic motion if \(x\) is displacement
(ii) SHM of angular frequency \(2 \omega\)

364205 Which one of the following equations of motion represents simple harmonic motion?