358638
A uniform magnetic field is restricted within a region of radius \(r\). The magnetic field changes with time at a rate \(\dfrac{d \vec{B}}{d t}\). Loop 1 of radius \(R > r\) encloses the region \(r\) and loop 2 of radius \(R\) is outside the region of magnetic field as shown in the figure below. Then the e.m.f. generated is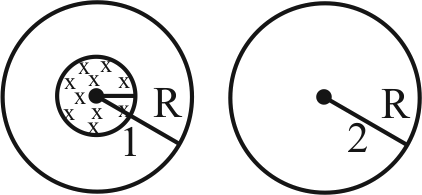
358638
A uniform magnetic field is restricted within a region of radius \(r\). The magnetic field changes with time at a rate \(\dfrac{d \vec{B}}{d t}\). Loop 1 of radius \(R > r\) encloses the region \(r\) and loop 2 of radius \(R\) is outside the region of magnetic field as shown in the figure below. Then the e.m.f. generated is
358638
A uniform magnetic field is restricted within a region of radius \(r\). The magnetic field changes with time at a rate \(\dfrac{d \vec{B}}{d t}\). Loop 1 of radius \(R > r\) encloses the region \(r\) and loop 2 of radius \(R\) is outside the region of magnetic field as shown in the figure below. Then the e.m.f. generated is
358638
A uniform magnetic field is restricted within a region of radius \(r\). The magnetic field changes with time at a rate \(\dfrac{d \vec{B}}{d t}\). Loop 1 of radius \(R > r\) encloses the region \(r\) and loop 2 of radius \(R\) is outside the region of magnetic field as shown in the figure below. Then the e.m.f. generated is
