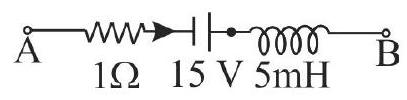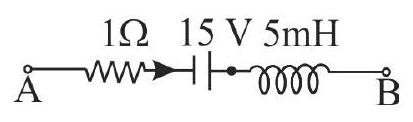358393
In given figure, \(R = 15\,\Omega ,L = 5.0\,H\), the ideal battery has \({\varepsilon=10 {~V}}\), and the fuse in the upper branch is an ideal \(3.0\,A\) fuse. It has zero resistance as long as the current through it remains less than \(3.0\,A.\) If the current reaches \(3.0\,A,\) the fuse "blows" and thereafter has infinite resistance. Switch \({S}\) is closed at time \({t=0}\). At what time does the fuse blow ?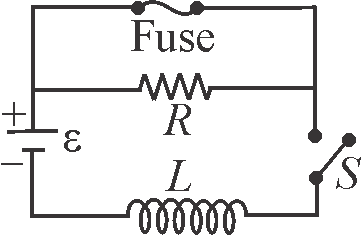
358394
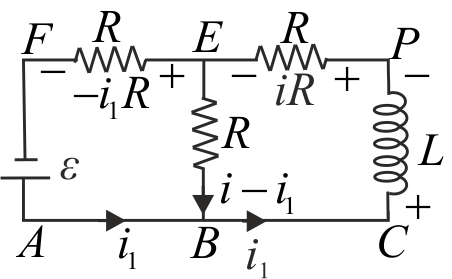
In the following circuit, the switch is closed at \({t}=0\). Initially, there is no current in inductor. The relation of current in the coil with time is given as \({i}=\dfrac{\varepsilon}{{NR}}\left[1-\exp \left(-{Q} \dfrac{{R}}{{L}} {t}\right)\right]\). What is the value of \(\dfrac{{N}}{{Q}}\) ?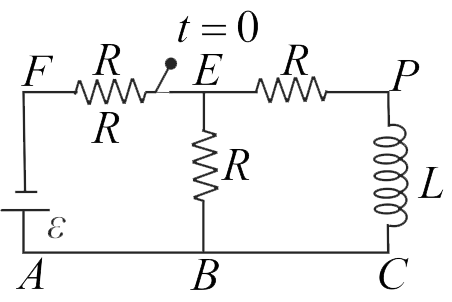
358393
In given figure, \(R = 15\,\Omega ,L = 5.0\,H\), the ideal battery has \({\varepsilon=10 {~V}}\), and the fuse in the upper branch is an ideal \(3.0\,A\) fuse. It has zero resistance as long as the current through it remains less than \(3.0\,A.\) If the current reaches \(3.0\,A,\) the fuse "blows" and thereafter has infinite resistance. Switch \({S}\) is closed at time \({t=0}\). At what time does the fuse blow ?
358394
In the following circuit, the switch is closed at \({t}=0\). Initially, there is no current in inductor. The relation of current in the coil with time is given as \({i}=\dfrac{\varepsilon}{{NR}}\left[1-\exp \left(-{Q} \dfrac{{R}}{{L}} {t}\right)\right]\). What is the value of \(\dfrac{{N}}{{Q}}\) ?
358393
In given figure, \(R = 15\,\Omega ,L = 5.0\,H\), the ideal battery has \({\varepsilon=10 {~V}}\), and the fuse in the upper branch is an ideal \(3.0\,A\) fuse. It has zero resistance as long as the current through it remains less than \(3.0\,A.\) If the current reaches \(3.0\,A,\) the fuse "blows" and thereafter has infinite resistance. Switch \({S}\) is closed at time \({t=0}\). At what time does the fuse blow ?
358394
In the following circuit, the switch is closed at \({t}=0\). Initially, there is no current in inductor. The relation of current in the coil with time is given as \({i}=\dfrac{\varepsilon}{{NR}}\left[1-\exp \left(-{Q} \dfrac{{R}}{{L}} {t}\right)\right]\). What is the value of \(\dfrac{{N}}{{Q}}\) ?
358393
In given figure, \(R = 15\,\Omega ,L = 5.0\,H\), the ideal battery has \({\varepsilon=10 {~V}}\), and the fuse in the upper branch is an ideal \(3.0\,A\) fuse. It has zero resistance as long as the current through it remains less than \(3.0\,A.\) If the current reaches \(3.0\,A,\) the fuse "blows" and thereafter has infinite resistance. Switch \({S}\) is closed at time \({t=0}\). At what time does the fuse blow ?
358394
In the following circuit, the switch is closed at \({t}=0\). Initially, there is no current in inductor. The relation of current in the coil with time is given as \({i}=\dfrac{\varepsilon}{{NR}}\left[1-\exp \left(-{Q} \dfrac{{R}}{{L}} {t}\right)\right]\). What is the value of \(\dfrac{{N}}{{Q}}\) ?