358079
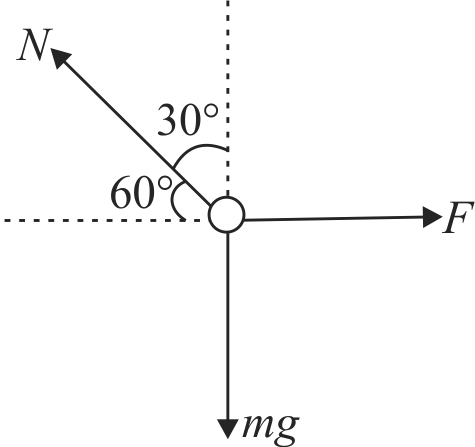
Two identical beads each having a mass \({m}\) and charge \({q}\). When placed in a hemispherical bowl of radius \({R}\) with frictionless, non-conducting walls, the beads move, and at equilibrium they are a distance \({R}\) apart (see figure). If the charge on each bead is found to be \({q=\left[\left(\dfrac{4 \pi \varepsilon_{0} m g R}{\sqrt{N}}\right)^{1 / 2}\right]}\), find the value of \({N}\).
358079
Two identical beads each having a mass \({m}\) and charge \({q}\). When placed in a hemispherical bowl of radius \({R}\) with frictionless, non-conducting walls, the beads move, and at equilibrium they are a distance \({R}\) apart (see figure). If the charge on each bead is found to be \({q=\left[\left(\dfrac{4 \pi \varepsilon_{0} m g R}{\sqrt{N}}\right)^{1 / 2}\right]}\), find the value of \({N}\).
358079
Two identical beads each having a mass \({m}\) and charge \({q}\). When placed in a hemispherical bowl of radius \({R}\) with frictionless, non-conducting walls, the beads move, and at equilibrium they are a distance \({R}\) apart (see figure). If the charge on each bead is found to be \({q=\left[\left(\dfrac{4 \pi \varepsilon_{0} m g R}{\sqrt{N}}\right)^{1 / 2}\right]}\), find the value of \({N}\).
358079
Two identical beads each having a mass \({m}\) and charge \({q}\). When placed in a hemispherical bowl of radius \({R}\) with frictionless, non-conducting walls, the beads move, and at equilibrium they are a distance \({R}\) apart (see figure). If the charge on each bead is found to be \({q=\left[\left(\dfrac{4 \pi \varepsilon_{0} m g R}{\sqrt{N}}\right)^{1 / 2}\right]}\), find the value of \({N}\).