358052
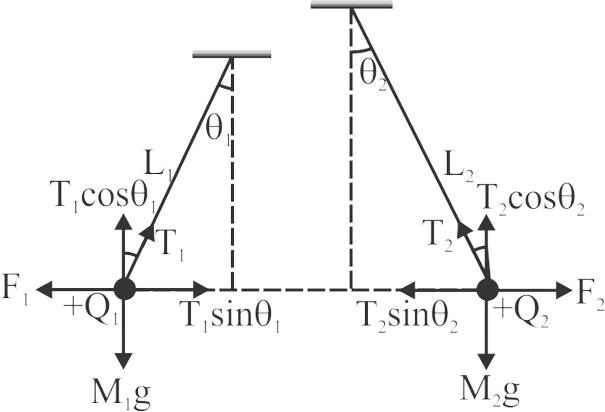
Two small spheres of masses \({M_1}\,{\rm{and}}\,{M_2}\) are suspended by weightless insulating threads of lengths \({L_1}\,{\rm{and}}\,{L_2}\) . The spheres carry charges \({Q_1}\,{\rm{and}}\,{Q_2}\) respectively. The spheres are suspended such that they are in level with one another and the threads are inclined to the vertical at angles of \({\theta _1}\,{\rm{and}}\,{\theta _2}\) as shown in figure. Which one of the following conditions is essential, if \({\theta _1}\, = \,{\theta _2}?\)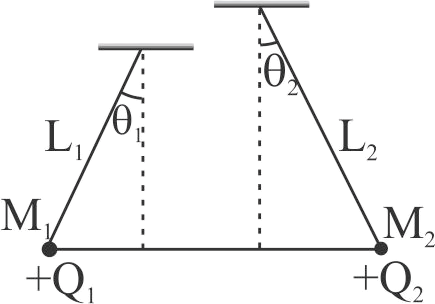
358053
Assertion :
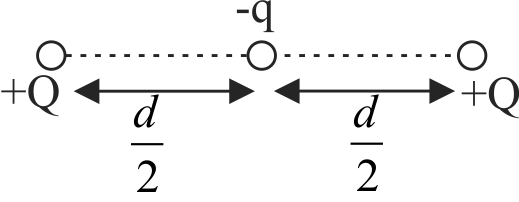
A charge is lying at the centre of the line joining two similar charges each which are fixed. The system will be in equilibrium if that charge is one fourth of the similar charges.
Reason :
For charge to be in equilibrium, sum of the forces on charge due to rest of the two charges must be zero.
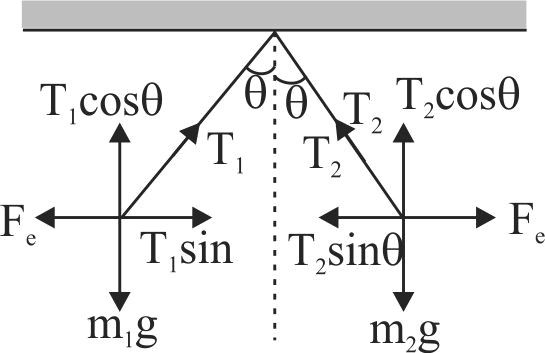
358056 Two positively charged spheres of masses, \({m_1}\,{\rm{and}}\,{m_2}\) are suspended from a common point at the ceiling by identical insulating massless strings of length \(l\). Charges on the two spheres are \({q_1}\,{\rm{and}}\,{q_2}\),respectively. At equilibrium both strings make the same angle \(\theta \) with the vertical.Then
358052
Two small spheres of masses \({M_1}\,{\rm{and}}\,{M_2}\) are suspended by weightless insulating threads of lengths \({L_1}\,{\rm{and}}\,{L_2}\) . The spheres carry charges \({Q_1}\,{\rm{and}}\,{Q_2}\) respectively. The spheres are suspended such that they are in level with one another and the threads are inclined to the vertical at angles of \({\theta _1}\,{\rm{and}}\,{\theta _2}\) as shown in figure. Which one of the following conditions is essential, if \({\theta _1}\, = \,{\theta _2}?\)
358053
Assertion :
A charge is lying at the centre of the line joining two similar charges each which are fixed. The system will be in equilibrium if that charge is one fourth of the similar charges.
Reason :
For charge to be in equilibrium, sum of the forces on charge due to rest of the two charges must be zero.
358056 Two positively charged spheres of masses, \({m_1}\,{\rm{and}}\,{m_2}\) are suspended from a common point at the ceiling by identical insulating massless strings of length \(l\). Charges on the two spheres are \({q_1}\,{\rm{and}}\,{q_2}\),respectively. At equilibrium both strings make the same angle \(\theta \) with the vertical.Then
358052
Two small spheres of masses \({M_1}\,{\rm{and}}\,{M_2}\) are suspended by weightless insulating threads of lengths \({L_1}\,{\rm{and}}\,{L_2}\) . The spheres carry charges \({Q_1}\,{\rm{and}}\,{Q_2}\) respectively. The spheres are suspended such that they are in level with one another and the threads are inclined to the vertical at angles of \({\theta _1}\,{\rm{and}}\,{\theta _2}\) as shown in figure. Which one of the following conditions is essential, if \({\theta _1}\, = \,{\theta _2}?\)
358053
Assertion :
A charge is lying at the centre of the line joining two similar charges each which are fixed. The system will be in equilibrium if that charge is one fourth of the similar charges.
Reason :
For charge to be in equilibrium, sum of the forces on charge due to rest of the two charges must be zero.
358056 Two positively charged spheres of masses, \({m_1}\,{\rm{and}}\,{m_2}\) are suspended from a common point at the ceiling by identical insulating massless strings of length \(l\). Charges on the two spheres are \({q_1}\,{\rm{and}}\,{q_2}\),respectively. At equilibrium both strings make the same angle \(\theta \) with the vertical.Then
358052
Two small spheres of masses \({M_1}\,{\rm{and}}\,{M_2}\) are suspended by weightless insulating threads of lengths \({L_1}\,{\rm{and}}\,{L_2}\) . The spheres carry charges \({Q_1}\,{\rm{and}}\,{Q_2}\) respectively. The spheres are suspended such that they are in level with one another and the threads are inclined to the vertical at angles of \({\theta _1}\,{\rm{and}}\,{\theta _2}\) as shown in figure. Which one of the following conditions is essential, if \({\theta _1}\, = \,{\theta _2}?\)
358053
Assertion :
A charge is lying at the centre of the line joining two similar charges each which are fixed. The system will be in equilibrium if that charge is one fourth of the similar charges.
Reason :
For charge to be in equilibrium, sum of the forces on charge due to rest of the two charges must be zero.
358056 Two positively charged spheres of masses, \({m_1}\,{\rm{and}}\,{m_2}\) are suspended from a common point at the ceiling by identical insulating massless strings of length \(l\). Charges on the two spheres are \({q_1}\,{\rm{and}}\,{q_2}\),respectively. At equilibrium both strings make the same angle \(\theta \) with the vertical.Then
358052
Two small spheres of masses \({M_1}\,{\rm{and}}\,{M_2}\) are suspended by weightless insulating threads of lengths \({L_1}\,{\rm{and}}\,{L_2}\) . The spheres carry charges \({Q_1}\,{\rm{and}}\,{Q_2}\) respectively. The spheres are suspended such that they are in level with one another and the threads are inclined to the vertical at angles of \({\theta _1}\,{\rm{and}}\,{\theta _2}\) as shown in figure. Which one of the following conditions is essential, if \({\theta _1}\, = \,{\theta _2}?\)
358053
Assertion :
A charge is lying at the centre of the line joining two similar charges each which are fixed. The system will be in equilibrium if that charge is one fourth of the similar charges.
Reason :
For charge to be in equilibrium, sum of the forces on charge due to rest of the two charges must be zero.
358056 Two positively charged spheres of masses, \({m_1}\,{\rm{and}}\,{m_2}\) are suspended from a common point at the ceiling by identical insulating massless strings of length \(l\). Charges on the two spheres are \({q_1}\,{\rm{and}}\,{q_2}\),respectively. At equilibrium both strings make the same angle \(\theta \) with the vertical.Then