358045
Electric field due to
Column I
Column II
A
Infinite plane sheet of charge
P
\(0\)
B
Infinite plane sheet of uniform thickness
Q
\(\frac{\sigma }{{2{\varepsilon _0}}}\)
C
Non -conducting charged solid sphere at its surface
R
\(\frac{{R\rho }}{{3{\varepsilon _0}}}\)
D
Conducting charged solid sphere at its centre
S
\(\frac{\sigma }{{{\varepsilon _0}}}\)
358046 A charged conductor produces an electric field of intensity \({10^3}V/m\) just outside its surface in vacuum. Then, it produces the electric field of intensity \(E\) just outside its surface, when it is placed in a medium of dielectric constant 4. The value of \(E\) will be
358048
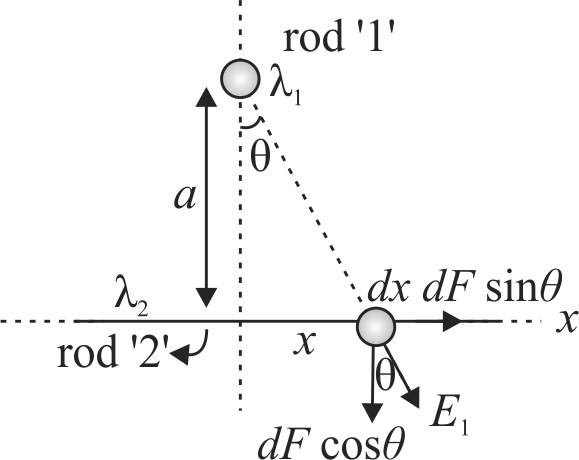
Two mutually perpendicular long straight conducting rods carrying uniformly distributed charges of linear charge densities \({\lambda_{1}}\) and \({\lambda_{2}}\) are positioned at a distance a from each other. If the force between the rods is found to be \({F_{\text {net }}=\dfrac{\lambda_{1} \lambda_{2}}{n \varepsilon_{0}}}\) find the value of \({n}\).
358045
Electric field due to
Column I
Column II
A
Infinite plane sheet of charge
P
\(0\)
B
Infinite plane sheet of uniform thickness
Q
\(\frac{\sigma }{{2{\varepsilon _0}}}\)
C
Non -conducting charged solid sphere at its surface
R
\(\frac{{R\rho }}{{3{\varepsilon _0}}}\)
D
Conducting charged solid sphere at its centre
S
\(\frac{\sigma }{{{\varepsilon _0}}}\)
358046 A charged conductor produces an electric field of intensity \({10^3}V/m\) just outside its surface in vacuum. Then, it produces the electric field of intensity \(E\) just outside its surface, when it is placed in a medium of dielectric constant 4. The value of \(E\) will be
358048
Two mutually perpendicular long straight conducting rods carrying uniformly distributed charges of linear charge densities \({\lambda_{1}}\) and \({\lambda_{2}}\) are positioned at a distance a from each other. If the force between the rods is found to be \({F_{\text {net }}=\dfrac{\lambda_{1} \lambda_{2}}{n \varepsilon_{0}}}\) find the value of \({n}\).
358045
Electric field due to
Column I
Column II
A
Infinite plane sheet of charge
P
\(0\)
B
Infinite plane sheet of uniform thickness
Q
\(\frac{\sigma }{{2{\varepsilon _0}}}\)
C
Non -conducting charged solid sphere at its surface
R
\(\frac{{R\rho }}{{3{\varepsilon _0}}}\)
D
Conducting charged solid sphere at its centre
S
\(\frac{\sigma }{{{\varepsilon _0}}}\)
358046 A charged conductor produces an electric field of intensity \({10^3}V/m\) just outside its surface in vacuum. Then, it produces the electric field of intensity \(E\) just outside its surface, when it is placed in a medium of dielectric constant 4. The value of \(E\) will be
358048
Two mutually perpendicular long straight conducting rods carrying uniformly distributed charges of linear charge densities \({\lambda_{1}}\) and \({\lambda_{2}}\) are positioned at a distance a from each other. If the force between the rods is found to be \({F_{\text {net }}=\dfrac{\lambda_{1} \lambda_{2}}{n \varepsilon_{0}}}\) find the value of \({n}\).
358045
Electric field due to
Column I
Column II
A
Infinite plane sheet of charge
P
\(0\)
B
Infinite plane sheet of uniform thickness
Q
\(\frac{\sigma }{{2{\varepsilon _0}}}\)
C
Non -conducting charged solid sphere at its surface
R
\(\frac{{R\rho }}{{3{\varepsilon _0}}}\)
D
Conducting charged solid sphere at its centre
S
\(\frac{\sigma }{{{\varepsilon _0}}}\)
358046 A charged conductor produces an electric field of intensity \({10^3}V/m\) just outside its surface in vacuum. Then, it produces the electric field of intensity \(E\) just outside its surface, when it is placed in a medium of dielectric constant 4. The value of \(E\) will be
358048
Two mutually perpendicular long straight conducting rods carrying uniformly distributed charges of linear charge densities \({\lambda_{1}}\) and \({\lambda_{2}}\) are positioned at a distance a from each other. If the force between the rods is found to be \({F_{\text {net }}=\dfrac{\lambda_{1} \lambda_{2}}{n \varepsilon_{0}}}\) find the value of \({n}\).
358045
Electric field due to
Column I
Column II
A
Infinite plane sheet of charge
P
\(0\)
B
Infinite plane sheet of uniform thickness
Q
\(\frac{\sigma }{{2{\varepsilon _0}}}\)
C
Non -conducting charged solid sphere at its surface
R
\(\frac{{R\rho }}{{3{\varepsilon _0}}}\)
D
Conducting charged solid sphere at its centre
S
\(\frac{\sigma }{{{\varepsilon _0}}}\)
358046 A charged conductor produces an electric field of intensity \({10^3}V/m\) just outside its surface in vacuum. Then, it produces the electric field of intensity \(E\) just outside its surface, when it is placed in a medium of dielectric constant 4. The value of \(E\) will be
358048
Two mutually perpendicular long straight conducting rods carrying uniformly distributed charges of linear charge densities \({\lambda_{1}}\) and \({\lambda_{2}}\) are positioned at a distance a from each other. If the force between the rods is found to be \({F_{\text {net }}=\dfrac{\lambda_{1} \lambda_{2}}{n \varepsilon_{0}}}\) find the value of \({n}\).