358029 A system consists of a uniformly charged sphere of radius \(R\) and a surrounding medium filled by a charge with the volume density \(\rho = \frac{\alpha }{r}\), where \(\alpha\) is a positive constant and \(r\) is the distance from the centre of the sphere. The charge of the sphere for which the electric field intensity \(E\) outside the sphere is independent of \(r\) is \(N \alpha R^{2}\). What is the value of \(N\)?
358030
A thin conducting ring of radius \(R\) is given a charge + \(Q\). The electric field at the centre \(O\) of the ring due to the charge on the part \(AKB\) of the ring is \(E\). The electric field at the centre due to the charge on the part \(ACDB\) of the ring is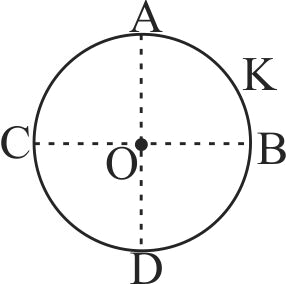
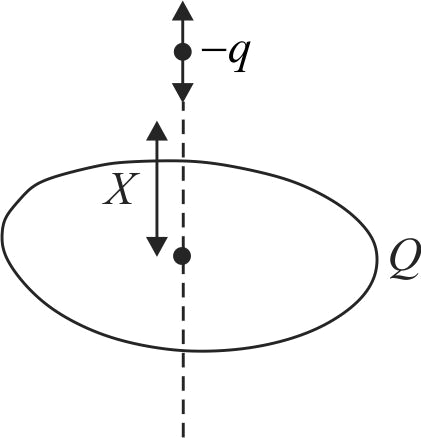
358031 Positive charge \(Q\) is distributed uniformly over a circular ring of radius \(R\). A point particle having a mass (m) and a negative charge \(q\) is placed on its axis at a distance \(x\) from the centre. Assuming \(x < R\), find the time period of oscillation of the particle, if it is released from there [neglect gravity]. \(\quad\)
358029 A system consists of a uniformly charged sphere of radius \(R\) and a surrounding medium filled by a charge with the volume density \(\rho = \frac{\alpha }{r}\), where \(\alpha\) is a positive constant and \(r\) is the distance from the centre of the sphere. The charge of the sphere for which the electric field intensity \(E\) outside the sphere is independent of \(r\) is \(N \alpha R^{2}\). What is the value of \(N\)?
358030
A thin conducting ring of radius \(R\) is given a charge + \(Q\). The electric field at the centre \(O\) of the ring due to the charge on the part \(AKB\) of the ring is \(E\). The electric field at the centre due to the charge on the part \(ACDB\) of the ring is
358031 Positive charge \(Q\) is distributed uniformly over a circular ring of radius \(R\). A point particle having a mass (m) and a negative charge \(q\) is placed on its axis at a distance \(x\) from the centre. Assuming \(x < R\), find the time period of oscillation of the particle, if it is released from there [neglect gravity]. \(\quad\)
358029 A system consists of a uniformly charged sphere of radius \(R\) and a surrounding medium filled by a charge with the volume density \(\rho = \frac{\alpha }{r}\), where \(\alpha\) is a positive constant and \(r\) is the distance from the centre of the sphere. The charge of the sphere for which the electric field intensity \(E\) outside the sphere is independent of \(r\) is \(N \alpha R^{2}\). What is the value of \(N\)?
358030
A thin conducting ring of radius \(R\) is given a charge + \(Q\). The electric field at the centre \(O\) of the ring due to the charge on the part \(AKB\) of the ring is \(E\). The electric field at the centre due to the charge on the part \(ACDB\) of the ring is
358031 Positive charge \(Q\) is distributed uniformly over a circular ring of radius \(R\). A point particle having a mass (m) and a negative charge \(q\) is placed on its axis at a distance \(x\) from the centre. Assuming \(x < R\), find the time period of oscillation of the particle, if it is released from there [neglect gravity]. \(\quad\)
358029 A system consists of a uniformly charged sphere of radius \(R\) and a surrounding medium filled by a charge with the volume density \(\rho = \frac{\alpha }{r}\), where \(\alpha\) is a positive constant and \(r\) is the distance from the centre of the sphere. The charge of the sphere for which the electric field intensity \(E\) outside the sphere is independent of \(r\) is \(N \alpha R^{2}\). What is the value of \(N\)?
358030
A thin conducting ring of radius \(R\) is given a charge + \(Q\). The electric field at the centre \(O\) of the ring due to the charge on the part \(AKB\) of the ring is \(E\). The electric field at the centre due to the charge on the part \(ACDB\) of the ring is
358031 Positive charge \(Q\) is distributed uniformly over a circular ring of radius \(R\). A point particle having a mass (m) and a negative charge \(q\) is placed on its axis at a distance \(x\) from the centre. Assuming \(x < R\), find the time period of oscillation of the particle, if it is released from there [neglect gravity]. \(\quad\)