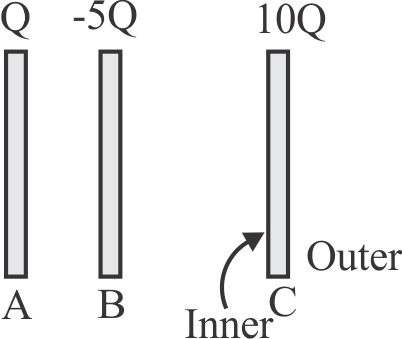
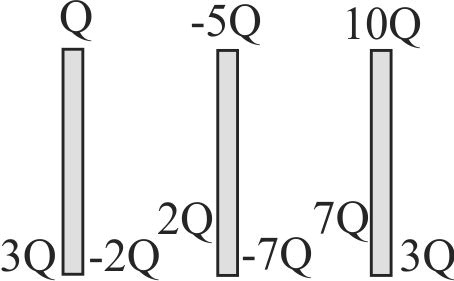
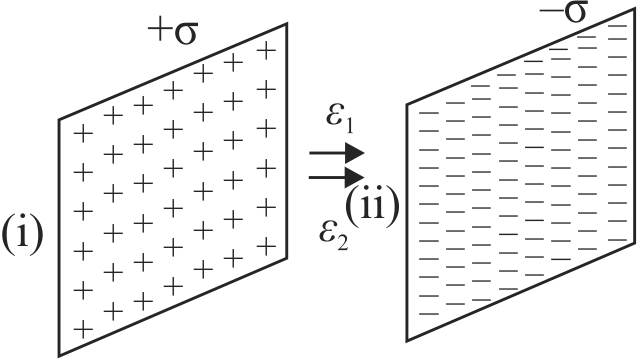
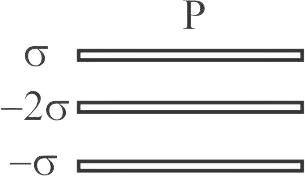
358025 Two infinitely long parallel conducting plates having surface charge densities \(+\sigma\) and \(-\sigma\) respectively, are separated by a small distance. The medium between the plates is vacuum. If \(\varepsilon_{0}\) is the dielectric permittivity of vacuum, then the electric field in the region between the plates is
358025 Two infinitely long parallel conducting plates having surface charge densities \(+\sigma\) and \(-\sigma\) respectively, are separated by a small distance. The medium between the plates is vacuum. If \(\varepsilon_{0}\) is the dielectric permittivity of vacuum, then the electric field in the region between the plates is
358025 Two infinitely long parallel conducting plates having surface charge densities \(+\sigma\) and \(-\sigma\) respectively, are separated by a small distance. The medium between the plates is vacuum. If \(\varepsilon_{0}\) is the dielectric permittivity of vacuum, then the electric field in the region between the plates is
358025 Two infinitely long parallel conducting plates having surface charge densities \(+\sigma\) and \(-\sigma\) respectively, are separated by a small distance. The medium between the plates is vacuum. If \(\varepsilon_{0}\) is the dielectric permittivity of vacuum, then the electric field in the region between the plates is