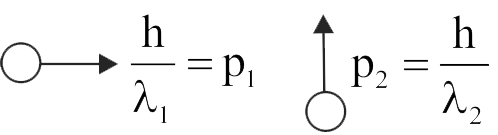357905 Two particles are moving at right angle to each other, and their de Broglie wavelengths are \({\lambda_{1}}\) and \({\lambda_{2}}\), respectively. The particles suffer perfectly inelastic collision. The de Broglie wavelength \({\lambda}\) of the final particle is given by
357907 A photon and electron have same de Broglie wavelength. Given that \(v\) is the speed of electron and \(c\) is the velocity of light. \(E_{e}, E_{p}\) are the kinetic energies of electron and photon respectively. \(p_{e}, p_{h}\) are the momentum of electron and photon respectively. Then which of the following relation is correct?
357905 Two particles are moving at right angle to each other, and their de Broglie wavelengths are \({\lambda_{1}}\) and \({\lambda_{2}}\), respectively. The particles suffer perfectly inelastic collision. The de Broglie wavelength \({\lambda}\) of the final particle is given by
357907 A photon and electron have same de Broglie wavelength. Given that \(v\) is the speed of electron and \(c\) is the velocity of light. \(E_{e}, E_{p}\) are the kinetic energies of electron and photon respectively. \(p_{e}, p_{h}\) are the momentum of electron and photon respectively. Then which of the following relation is correct?
357905 Two particles are moving at right angle to each other, and their de Broglie wavelengths are \({\lambda_{1}}\) and \({\lambda_{2}}\), respectively. The particles suffer perfectly inelastic collision. The de Broglie wavelength \({\lambda}\) of the final particle is given by
357907 A photon and electron have same de Broglie wavelength. Given that \(v\) is the speed of electron and \(c\) is the velocity of light. \(E_{e}, E_{p}\) are the kinetic energies of electron and photon respectively. \(p_{e}, p_{h}\) are the momentum of electron and photon respectively. Then which of the following relation is correct?
357905 Two particles are moving at right angle to each other, and their de Broglie wavelengths are \({\lambda_{1}}\) and \({\lambda_{2}}\), respectively. The particles suffer perfectly inelastic collision. The de Broglie wavelength \({\lambda}\) of the final particle is given by
357907 A photon and electron have same de Broglie wavelength. Given that \(v\) is the speed of electron and \(c\) is the velocity of light. \(E_{e}, E_{p}\) are the kinetic energies of electron and photon respectively. \(p_{e}, p_{h}\) are the momentum of electron and photon respectively. Then which of the following relation is correct?